
Direction of change and entropy
 |
Direction of change and entropy |
We are immersed in change. Some changes take less than a second—explosion of fuel in an internal combustion engine. Others may take years—growth of a tree from seedling to stately shade. And still others can take millions of years—transformation of sedimentary to metamorphic rock. We are in a period of climate disruption that involves changes at all these time scales. Regardless of their speed, a fundamental question about changes is: Why these? What determines the direction of the changes we observe? Energetics?
Entropy is the property that indicates and predicts the direction of all change. So, since change is so important, understanding entropy is also important. The concept of entropy often seems mysterious and difficult to understand, but this may reflect the way it is usually first presented—either incorrectly as having something to do with “disorder” (an unclear and unquantifiable concept), or via the macroscopic, classical thermodynamic path that usually provides little connection to tangible systems (except heat engines).
This description points the way toward another approach, based on an atomic-molecular level model, which gives a “feel” for entropy and its universal applications without getting bogged down in too much math. (The model can be developed quantitatively at a more sophisticated level, statistical thermodynamics, but that is unnecessary at the beginning.) Because the approach is likely to be unfamiliar, we will work through it together, as you respond to each question. |
|||||
A. Probability model for direction of change |
|||||
Consider an isolated system (one that does not exchange energy or mass with its surroundings) that can exist in more than one observable state (mixed or unmixed, for example). Spontaneous changes will be in the direction toward the most probable state. The number of distinguishable arrangements of the energy that give a particular state of the system is a measure of the probability that this state will be observed. A new arrangement is distinguishable from another if you turn your back, a rearrangement occurs, and you can tell the new arrangement from the original when you look again at the system. Our fundamental assumption is that each distinguishably different arrangement of a system is equally probable. |
|||||
Whoa! OK, there is a huge amount to swallow here. And even more as we consider what these terms and concepts mean. Some of this will become more clear as we consider specific models. It does seem to be common sense that a system that can change will change in a direction that will make it more/most probable. The difficulties are in defining this probability and some way to measure and/or calculate it. The choice, for this model, is to associate probability with the number of ways to “arrange the energy” in the system of interest. Thinking about energy arrangements takes up a large part of the rest of this Activity. The “fundamental assumption” of this model is just that, an assumption that cannot be proved. The only evidence that it is correct and valid is if the model gives correct answers for systems we already know about. Then we can have confidence about applying it to unfamiliar systems. |
|||||
Probability Since probability is at the heart of this model and since most of us don’t usually have daily contact with probability arguments, we’ll first consider a simple case that contains the elements of arrangements and probability that will be used later. We will use the symbol W to denote the number of distinguishable Ways that energy (or sometimes other things) can be arranged in a system. (This is the symbol often used in statistical thermodynamics for the number of microstates—equivalent to distinguishable arrangements—of a system.) |
|||||
1.
|
Consider a system that consists of two separate parts. Part A has one object in two boxes, while Part B has two identical objects in three boxes. 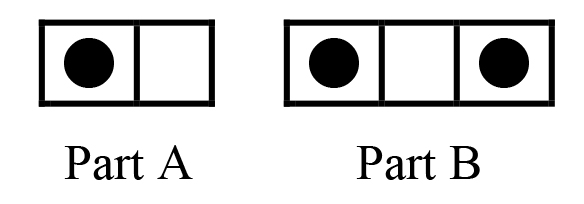 a) How many distinguishable arrangements are there for part A? WA = b) How many distinguishable arrangements are there for part B? WB = c) How many distinguishable arrangements, Wsystem, are there for the whole system? (Hint: Each arrangement of part A can be paired with any of the arrangements of part B.) One arrangement of the system is shown. Show all the others. 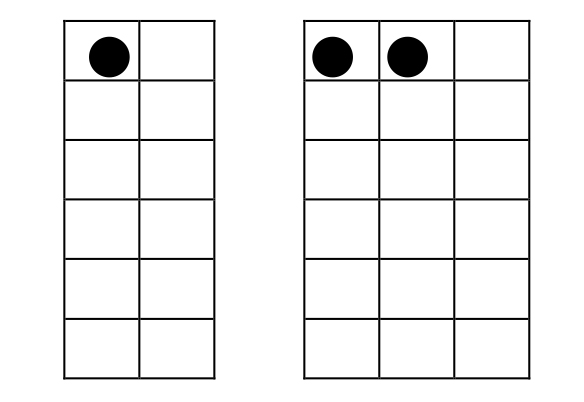 d) Write an algebraic expression relating Wsystem to WA and WB. Explain clearly why you choose this expression. |
||||
The expression you wrote relating Wsystem to WA and WB in item 1.d is an example of how the distinguishable arrangements of independent parts of any system are combined to give the total number of distinguishable arrangements for the whole system. Other combinatorial reminders will be introduced as they are needed. |
|||||
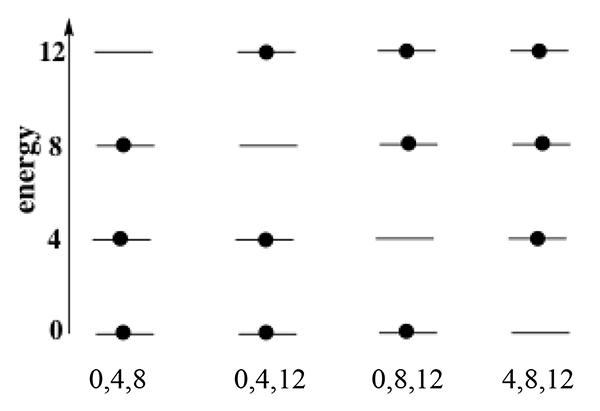
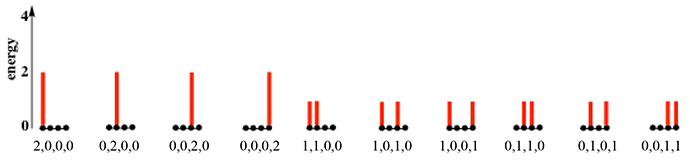
Energy in atomic-molecular level systems At the atomic-molecular level, all energies are quantized. That is, an atom or molecule can have only certain energies and no others. A common way to represent these energies is an energy level diagram in which horizontal lines represent the allowed energies, with the lines arranged in a “ladder” of increasing energy. The diagram here represents a system of three identical particles each of which can have one of four, equally-spaced allowed energies. |
|||||
 |
|||||
Each individual ladder shows a possible arrangement of the energy in the system. Sometimes, we say that a particle “occupies” a particular energy level, as though the particle were in a box. This is often useful in thinking about arrangements and probabilities, but you have to be careful to remember that this is shorthand, not physical reality. |
|||||
2.
|
Four arrangements of the energies among the particles are shown. Are they distinguishable? How do you know? Are others possible? Explain your response. |
||||
Although it’s imaginary, it is useful to have at least a mental picture of a physical system represented by this model. It could be a very tiny volume of gas containing three identical particles (atoms or molecules). If, as time passes, we make many observations of the energy distribution of the particles, we will always find them in one or another of the distributions in the diagram. Since there are four equally probable arrangements (equally probable by our fundamental assumption that all distinguishable arrangements are equally probable), we will find each arrangement in one quarter of the observations as they rapidly interchange. The energy properties of the system as a whole are an average of those corresponding to the individual distinguishable arrangements. |
|||||
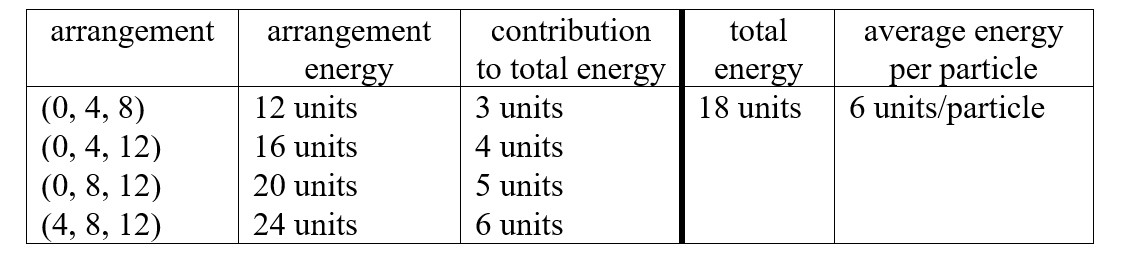
Another way to represent the distinguishable arrangements in a system like this is to list the energies of the particles, as shown below each ladder in the diagram. This makes it easier to do the analysis of their average, represented by this table and following discussion. |
|||||
 |
|||||
The four possible distinguishable arrangements and the energy of each are shown in the first and second columns of the table. (For our purposes, the actual energies are not relevant. Only their energies relative to one another are important, so we simply use numbers of “units” to specify this ordering. The values here are chosen to make our further discussion easier.) Since there are four equally probable arrangements, we divide the energy of each one by four to get its contribution to the total energy of the system and then sum the resulting values to get the total energy, 18 units, and the average energy per particle, 6 units/particle. |
|||||
3.
|
The following diagram represents one arrangement of a system of three identical particles each of which can have one of five, equally-spaced allowed energies. (The energy “units” in this diagram are the same as those in the previous one. The system here could be the same sample of gas, three particles, as before, but in a larger volume. The energy spacing is inversely proportional to the volume—larger volume, smaller spacing.) Find the other distinguishable arrangements and complete the analysis table that is started for you. (The third column cells cannot be filled in until you know the number of distinguishable arrangements.) |
||||
|
|||||
4.
|
How many distinguishable arrangements are possible? How do the values in your last two columns compare with those in the previous table for the system with larger energy spacing? Did you expect this? Explain why or why not. |
||||
B. Countable systems and reality |
|||||
The two systems shown in the previous section are called “countable systems”, because the distinguishable energy arrangements in them are easily counted, often with schematic diagrams like we used. But these are imaginary systems in the sense that we cannot (yet) see or manipulate a system of three molecular-level particles nor constrain them to simple energy ladders. So, why bother, unless they can somehow be related to systems we can observe? We start by determining the direction of change in a countable system, as some property of the system is changed. Then we apply what we have learned about directionality to real systems where an analogous property is changed. We can also turn the tables and start with a real system property and emulate it with a countable system to see what changes would be expected if the property changes. The systems in the previous section can be related to the properties of an ideal gas, if we know something about the translational energies available to the molecules. A quantum mechanical treatment of the translational energies shows that the spacing between energy levels is very tiny. (For practical purposes, at the macroscopic level, the energies are often simply considered as continuous, because there is no instrument capable of measuring the small differences. For our purposes, the small differences make it possible to create a countable system we can work with.) Even in a real gas, there are so many energy levels available that the likelihood of two molecules being in the same energy level is vanishingly small. Thus, every molecule is in a different energy level, just as we have chosen for the countable systems above. For mathematical ease, we have chosen to limit the number of energy levels available and simply made it a rule that only one particle may “occupy” any particular energy level. Further, even though the energy levels are very close, they get even closer as the volume occupied by a sample of gas increases. Thus, the system with three-unit spacing between the levels represents the gas in a larger volume compared to the one with four-unit spacing—the gas has expanded. |
|||||
5. |
Consider this divided container that initially contains a gas on one side of the divider and a vacuum on the other. When the divider is removed, the gas immediately expands to fill the entire container. Is this expected? How, if at all, do the results in the previous section predict this direction of spontaneous change? Clearly explain your reasoning. |
||||
 |
|||||
6. |
The temperature of a gas is proportional to the average translational energy of its molecules. How does the temperature of the particles (assumed to be a gas) in the previous section respond to expansion into a larger volume? What do you predict about the temperature of the expanded gas in item 5 compared to its original temperature? Clearly explain the reasoning for your responses. |
||||
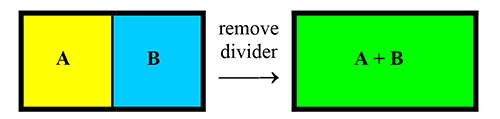
Mixtures Consider the change represented by this illustration. A and B are gases at the same temperature. (Colors make the illustration more attractive. Mixing yellow plus blue giving green is meant to evoke the idea that the molecules in the mixture are completely intermixed with one another.) |
|||||
 |
|||||
| One statement of Dalton’s law of partial pressures says that, in a mixture of gases, the gases act as a vacuum to each other (that is, each gas acts as if it were alone in the container). | |||||
7. |
Let WA be the number of ways to arrange the A particle energies in the separate volume on the left and WAmix the number of ways to arrange the A particle energies in the larger combined volume on the right, with analogous definitions for WB and WBmix. a) Is WAmix > WA or WAmix = WA or WAmix < WA? Give the reasoning for your response. b) Is WBmix > WB or WBmix = WB or WBmix < WB? Give the reasoning for your response. c) What is Wseparated, the total number of ways to arrange the separated particles in the left-hand container? Explain your reasoning. (Recall how the number of distinguishable arrangements for independent parts of a system are combined to give the total number of distinguishable arrangements for the whole system.) d) What is Wmixture, the total number of ways to arrange the separated particles in the right-hand container? Explain your reasoning. e) Is Wmixture greater than, equal to, or less than Wseparated? Explain your reasoning. f) Does your analysis suggest that the change illustrated above is spontaneous or non-spontaneous? Explain your reasoning. Does your experience in the “real world” confirm your response? Is there a general principle here? |
||||
C. Entropy |
|||||
You have worked with a few examples of and have some familiarity with a probability model for predicting the direction of changes. Since the predictions, spontaneous gas expansion into a vacuum and spontaneous mixing of gases, match the changes we actually observe, they are evidence (not, in themselves, proof) that the model has validity. The next step, taken by Ludwig Boltzmann (Austrian physicist, 1844-1906) relates this probability model to a thermodynamic property, entropy, always symbolized as S. The Boltzmann relationship (engraved on the headstone of his tomb in Vienna) is S = k lnW Here, lnW is the natural logarithm (base e) of the system’s number of distinguishable energy arrangements and k (= 1.38 x 10-23 J/K) is a proportionality constant, now called the Boltzmann constant, that appears over and over in descriptions of atomic-molecular systems. (In descriptions of macroscopic systems, k is multiplied by Avogadro’s number giving, NAk = R, the familiar gas constant.) To get familiar with entropy, we’ll start with the mixing example from the previous section. Using the Boltzmann relationship for the separated gases, we have |
|||||
SA = k lnWA |
|||||
This is a powerful result—the entropy of a system with several independent parts is the sum of the entropies of the individual parts. This is a result of the logarithmic relationship—numbers of distinguishable energy arrangements, which combine multiplicatively, give entropies that combine additively. Understanding direction of change is a central focus of this activity, so let’s examine the change in entropy for the mixing. When we discuss the properties of a system as it changes, we compare the final state of the system to the initial state—their difference, denoted by Δ, is always final minus initial. Thus, for the mixing, we have |
|||||
|
|||||
Another powerful result, due to logarithms, that allows us to determine the sign of an entropy change, ΔS, from the ratio of final to initial energy arrangements (simply knowing which is larger). |
|||||
8. |
Is ΔSmixing positive (> 0) or negative (< 0)? Clearly explain your response (based on your results in item 7). Is there a general principle here? |
||||
|
The symbol S for entropy seems odd, but it can be useful if you think of it as a measure of “Spreadedness”. How “spread out” is the system’s energy? How many distinguishable arrangements of its energy are possible? Entropy and energy are intimately related. Essentially nothing can happen, no changes can occur, without energy being involved. Energy is always conserved in these changes, but the only spontaneous changes that can occur are those that increase the number of distinguishable arrangements of the energy involved, that is, increase the entropy. The first and second laws of thermodynamics are embodied in these statements. |
||||
D. Revisiting probability and countable systems |
|||||
It’s often convenient to use countable systems larger than those we have introduced so far. You can see how tedious it would be to have to draw out the kind of diagrams we have been using to determine the number of distinguishable arrangements. And deciding whether you had them all would be very difficult. We need a more analytical way to find W for larger systems. The number of ways, WN,n, of distributing n identical objects among N boxes (n ≤ N), where each box may hold only one object is |
|||||
|
|||||
Thus, the number of distinguishable arrangements of three objects in five boxes, W5,3 is |
|||||
This is the result you got by actually drawing diagrams to find the number of distinguishable arrangements of three particles among five energy levels, where each particle must have a different energy. |
|||||
9. |
Find the number of distinguishable arrangements of three particles among four energy levels, where each particle must have a different energy. Do you get the result you know from the previous sections? |
||||
10. |
Find the number of distinguishable arrangements of nine identical objects among |
||||
It’s appropriate to set up the Osmosis Activity here. |
|||||
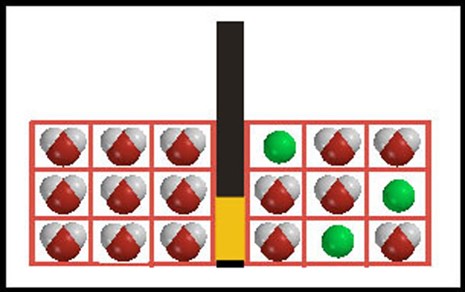
Entropy and osmosis This illustration is designed to represent a system in which osmosis can occur. A barrier, part of which is semi-permeable, separates the two chambers. Water molecules (space-filling model representations) can pass through the semi-permeable barrier, but the solute molecules (represented by green balls) cannot. |
|||||
 |
|||||
To analyze this system, we need a model for the way energy is distributed among these molecules. This is complicated in a liquid where there are strong interactions among molecules, but we can simplify by considering only the mixing aspect of the system and assuming we can treat the “boxes” (cells) in each chamber as energy levels (drawn like this, instead of in a column, so they look more like a physical apparatus.) Each energy level can be “occupied” by a single molecule. With this assumption, the number of distinguishable energy arrangements on the solution side (right side) of the barrier is |
|||||
11. |
What is Wsolvent, the number of distinguishable energy arrangements on the solvent side (left side) of the barrier? |
||||
12. |
What is total number, Wtotal, of distinguishable energy arrangements for the system? Explain. |
||||
Since the barrier is permeable to water, water molecules can pass in either direction through the barrier. The direction of net flow, that is, an observable change in the system, depends on which direction gives a positive entropy change. Consider these two possible new states of the system, where three water molecules (net) have crossed the barrier, either from solvent to solution (A) or from solution to solvent (B). |
|||||
A 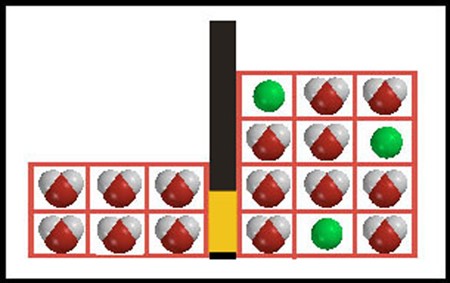 B B 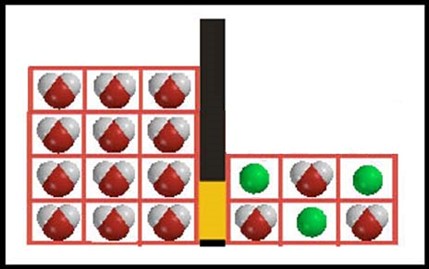 |
|||||
13. |
What is total number of distinguishable energy arrangements for system state A? |
||||
14. |
What is total number of distinguishable energy arrangements for system state B? |
||||
15. |
What is the sign of the entropy change, ΔS→A, for the change from the original state of the system to state A? What is the sign of the entropy change, ΔS→B, for the change from the original state of the system to state B? What is the direction of spontaneous change for osmosis? Clearly explain your responses. |
||||
In a more general case, instead of a pure solvent and solution, you may have a semi-permeable barrier separating two solutions of different concentrations. As you might expect, the spontaneous direction of water movement will be to equalize the solution concentrations (almost as though the membrane was not present). Water will move from the lower to higher concentration solution. A countable-system example is given in the Appendix. Complete the Osmosis Activity. |
|||||
D. Entropy and energy transfer |
|||||
Up to this point, we have considered only systems in which changes occurred without transfers of energy. But almost all chemical reactions involve transfer of energy—either releasing thermal energy to the surroundings (exothermic) or gaining it from the surroundings (endothermic). To begin analyzing the spontaneous direction of change when thermal energy changes are part of the process, start with the countable system distinguishable arrangements illustrated in this diagram. |
|||||
 |
|||||
The system is a four-particle solid (analogous to a macroscopic piece of metal, for example). The particles are fixed in place in the crystal structure of the solid—their positions distinguish them from one another. Thermal energy in the system causes the particles to vibrate, but their energies are quantized. They have to take up or give up energy only in discrete amounts (quanta). This example system contains two energy quanta. Vertical red bars represent a particle’s vibrational energy—zero, one, or two fundamental one-energy-unit quanta. The more quanta a particle has, the faster it vibrates. Energy arrangements can also be noted as shown below each diagram. This is, once again, a countable system for which the number of distinguishable arrangements is analogous to placing objects in boxes. In this case, each box (particle) can hold as many objects (quanta) as are available, which substantially increases the possible arrangements. This is rather like fruit-basket-upset where all the particles (N) and quanta (n) are mixed together and then picked out randomly and arranged in a line where the energy quanta go with the nearest particle to their left, like this one for the four-particle-two-quanta system above. |
|||||
There are (N + n)! possible arrangements, but there is a restriction. The first item in the line has to be a particle, since energy quanta must have a place to go and not be hanging out at the left end. The first selection from the pile of particles and quanta must be a particle, so this is not a random choice. Having chosen a particle, there are only (N–1) particles left in the pile, so the number of possible arrangements is [(N–1) + n]! [usually written (N+n–1)!]]. Just as in the former analysis of possible arrangements, many of these are not distinguishable, because they are only exchanges of identical items (particles or quanta). We account for this redundancy by dividing out such rearrangements, for a final WN,n relationship. |
|||||
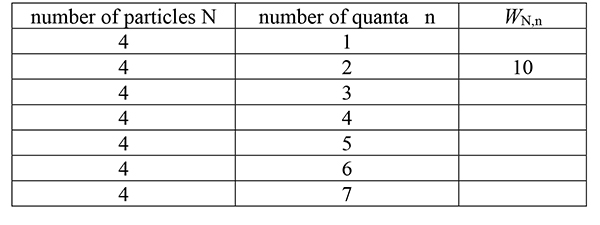
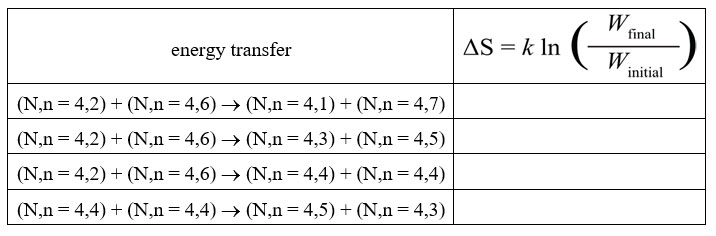
16. |
Complete this table to provide data for further analyses of energy transfers. |
||||
 |
|||||
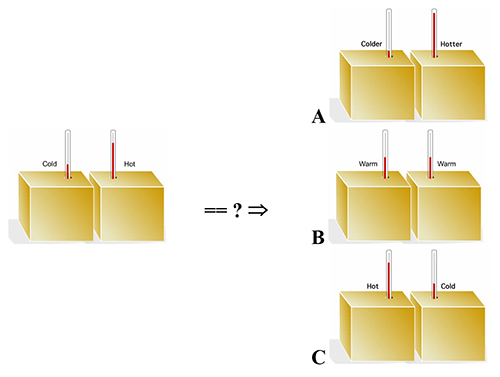
17. |
What is likely to result, if two identical blocks of metal, one hot and one cold, are brought together and allowed to exchange energy before separating again? What is your reasoning? |
||||
 |
|||||
18. |
Calculate ΔS (as a multiple of k) for each of the energy transfers between two identical four-particle solids shown in this table. Explain how, if at all, the results are related to your reasoning in item 17. Does this provide further evidence for the validity of the entropy model based on number of distinguishable arrangements of energy? Explain why or why not. |
||||
 |
|||||
Solids, liquids, and gases Pause for a moment to consider why there is a difference between the way we’ve treated the energy distributions in gases and solids. In gases, the translational energy levels are so closely packed that there are vastly more of them than there are particles, so each level is “occupied” by a single particle. Energy arrangements count the number of ways, W, identical particles can occupy the energy levels. There are a very large number of ways, so the entropy of a gas is large. In a solid, the particles are mostly restricted to vibrational motion about their fixed position. Identical particles in a solid are distinguishable by their position, so distinguishable arrangements are different distributions of identical energy quanta among them. Vibrational energy level spacings are large compared to the translational levels in a gas. For the same amount of total energy, there are fewer energy quanta and fewer ways to distribute them in a solid than a gas. The entropies of solids are relatively small: Ssolid < Sgas for the same compound. Liquids are an intermediate and more difficult phase to characterize. The particles can move about, but are far less free to do so than in a gas. The energy levels are associated with vibrational, rotational, and translational motions all mixed together with average spacings smaller than for a solid, but larger than in a gas: Ssolid < Sliquid < Sgas for the same compound. These entropies pose an important question. If gases have the highest entropy, why does any matter exist as solid or liquid? |
|||||
F. Energy, temperature and entropy relationship |
|||||
19. |
Consider these two changes for identical four-particle solids: (a) Find the entropy changes, ΔSA and ΔSB, for the two changes. Which entropy change is larger? (b) Find the entropy changes, ΔS-A and ΔS-B, for the reverse of the two changes (loss of one quantum). Which entropy change is larger? (c) How do the temperatures of the two systems, A and B, compare? Explain the reasoning for your response. |
||||
The results in item 19 are universal: for an energy change, ΔE (either positive or negative), in a system at two different temperatures, the entropy change is larger at the lower temperature. That is, for a system undergoing only an energy change, the entropy change is an inverse function of its temperature. (Sometimes an analogy helps to remember an idea. In this case, think about giving $5 to a person who only has $10 and another who has $100. The $5 will make a good deal more difference to the person who has less to begin with. So it is with energy, temperature, and entropy.) A relationship that embodies (at least qualitatively) the results of item 19 is |
|||||
You found that an increase in energy, ΔE > 0 (adding a quantum of energy), increased the entropy of the system, ΔS > 0, and conversely for a decrease in energy. Thus the sign of ΔS and ΔE is the same for a system where gain or loss of energy is the only change. And the entropy change is inversely proportional to the kelvin temperature of the system. Now, without proof, we will take this as the quantitative relationship among energy, temperature, and entropy. This can be proved rigorously, but we will not do so. You usually see this relationship expressed in terms of enthalpy change, ΔH, instead of ΔE, but, for changes in condensed phases—solids and liquids—ΔH and ΔE are essentially the same. |
|||||
This relationship (pointed to by analyses of countable systems) is fundamental to analyses of observable, macroscopic systems. A good example is the analysis of factors that affect phase change. Consider two systems: an ice-water mixture and an ice-salt-water solution mixture. If these mixtures are stirred until their temperatures are reasonably constant, how will their temperatures compare? You can find out by doing the Freezing point of a solution Activity. |
|||||
Looking back and ahead Recall that we began this Activity with the observation that one substance readily dissolved exothermically and another dissolved endothermically. So we concluded that the direction of energy transfer is not a predictor of the direction of change. Both endothermic and exothermic reactions occur (are spontaneous). We assume that change occurs in the direction that gives a more probable state of the system and measure relative probabilities in terms of the number of distinguishable arrangements of energy in the system. Defining entropy as a function of the number of distinguishable energy arrangements leads to a positive change in entropy as the criterion for direction of spontaneous change. We can infer that both dissolution reactions have a positive change in entropy, but we do not yet have a molecular level model that explains why one is exothermic and the other endothermic. That issue is explored in Reaction energies and entropies. |
|||||
Appendix |
|||||
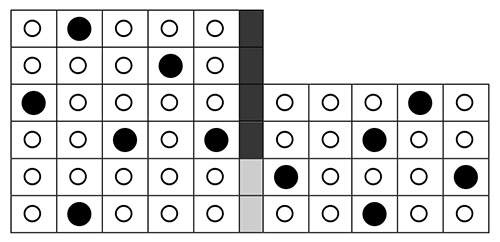
A more general case of osmosis. Instead of a pure solvent and solution, you may have a semi-permeable barrier separating two solutions of different concentrations. Open circles represent water molecules; filled circles represent solute molecules. |
|||||
 |
|||||
• |
What are the concentrations
on the left and right side? Express the results as decimals with two significant figures. Cleft = Cright = |
||||
• |
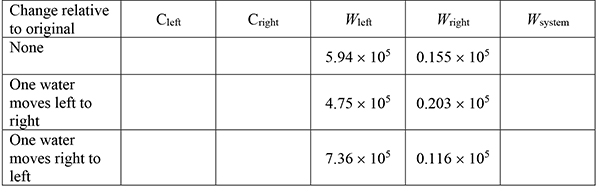
Complete this table for the original system shown above, as well as for the case that one molecule of water moves from left to right and for the case that one water molecule moves from right to left. (The analytical equation involving N and n was used to calculate number of arrangements given here for the solutions on the left and right. You might check to see that columns 4 and 5 are correct and to get practice with factorials.) |
||||
 |
|||||
• |
Which way, if any, will water move spontaneously across the barrier? Give the reasoning for your answer. |
||||
• |
How is osmosis related to the concentrations of the solutions on either side of the semi-permeable barrier? Explain your reasoning based on the above example. |
||||
• |
Show that ΔSsystem > 0, for the spontaneous process of osmosis in the above example. |
||||
 |
|||||
Instructor/presenter notes |
|||||
The content of this Activity and much of its companion, Reaction energies and entropies, is likely to be unfamiliar to almost everyone in your classroom, so they are presented in a more didactic way than any of the others. You should allow at least three class periods to complete this Activity, and two more, if you choose to incorporate the entropy-based Activities, Osmosis and Freezing point of a solution, as these colligative properties are introduced. At least a further three periods should be allowed for the second entropy Activity. The reward for taking time to introduce this atomic-molecular level entropy model and its applications is providing a “feel” for the concept and a way to visualize it that goes far beyond the hand-waving that characterizes too many introductions. It’s empowering to understand the direction of change at a fundamental level. The activity in the Introduction is included to demonstrate that some readily soluble compounds dissolve exothermically and others endothermically, so energetics does not provide a criterion for ready chemical change (or spontaneity). The set-up and analysis for the activity are:
|
|||||
After the groups have carried out the procedure described in the worksheet, get two or three groups to describe what they observed—dissolution of both white solids with one solution getting warm/hot and the other cool/cold. And what that means—energy/heat was released from one of the dissolution changes and, more subtly, energy was required from the surroundings (mainly the water itself; thus cooling it) to dissolve the other. Thus, everyone should conclude that energy change cannot be used to explain the direction of change. There are no other secondary chemistry textbooks and very few introductory college chemistry texts that we know of that have as succinct and correct a definition of entropy as that given in the material for the International Baccalaureate secondary curriculum. Our task in this Activity is to develop at least a semi-quantitative way (or ways) to find “the distribution of available energy among the particles”, so we can use entropy change to explain and predict the direction of change in the world around us. |
|||||
Part A |
|||||
1. |
a) There are two distinguishable arrangements, WA = 2, of one object in two boxes b) There are three distinguishable arrangements, WB = 3, of two objects in three boxes c) There are six distinguishable arrangements, Wsystem = 6, of the two systems together. d) Wsystem =WA×WB = 2 × 3 = 6. Multiplying the numbers of distinguishable arrangements for the independent parts A and B is the only mathematical combination that gives the total number of arrangements for the combined system. (In particular, the combination is not additive. Wsystem =WA+WB = 2+3 = 5, is incorrect.) This multiplicative combination is a fundamental property for combination of the distinguishable arrangements of independent parts of any system to give the total number of distinguishable arrangements for the whole system. If your students are already familiar with this sort of multiplicative combination, this item is a quick reminder to get them ready for more. If not, then try to be sure, probably through class discussion, that the lesson here is understood by each student. |
||||
2. |
The only way to tell whether the four arrangements are distinguishable is to compare each one with all the others to see whether it is different. This is easy to do almost at a glance with so few arrangements. To tell that these are the only arrangements possible, focus on the “empty” energy level. There is one empty level among the four available—that is, one “object” (empty level) to distribute among four “boxes” (the number of levels available). There are four arrangements of one object in four boxes and these are shown in the diagram as the empty level is in a different location in each arrangement. |
||||
The worksheet says the spacing between energy levels available for our particles in a tiny volume decreases (levels get closer together) as the volume of the space increases. This is a result of the wave properties of atomic level matter postulated by de Broglie. A simplified approach catches the essence of the argument. Planck proposed a particle-like relationship between electromagnetic wavelength and energy and de Broglie sort of reversed the reasoning, proposing wave properties associated with the kinetic energy, KE, of particles |
|||||
To get particle wavelengths, we choose the model of a particle in a one-dimensional box illustrated here. In this model, the particle moves only in a straight line from side to side of the box. (It’s not hard to extend the model to a three-dimensional box, but unnecessary for our purpose.) The waveform chosen to represent the matter wave is a sine wave. The criterion for a wave to represent a particle is that the amplitude of the wave has to be zero at the walls of the box; that is, it’s contained within the box. An infinite number of waves meet this criterion; the first five, labeled 1 through 5, are shown in the diagram. The wavelength of a wave is the distance along its line of travel required for a complete cycle of the wave. Expressed in terms of its “n” value and the length of the box, L, the wavelengths are (Be sure this make sense to you.) Substitute these particle wavelengths into the de Broglie relationship (after dividing both sides by v, the velocity) to get, Multiply both sides of this equation by two and then square both sides, Divide both sides by 2m to get, finally, For a given mass particle confined in a given size box, the expression inside the parentheses is a constant. The only energies allowed to the particle are n2 multiples of this constant, where n = 1, 2, 3, etc. This quantization of energies at the atomic-molecular level is a natural consequence of the treatment of particles as matter waves. Since L2 is in the denominator of the parenthetical expression, the allowed energies and the spacing between successive energies gets smaller for a larger L, larger box (volume in the three dimensional case), which is what we set out to show. If you choose to introduce any of this reasoning to your class, be careful to specify that the only relationships to the model chosen in the worksheet are the quantization of energy levels and the directional dependence of these energies on the volume enclosing the particles. The particle-in-a-box does not have equally spaced energy levels, as you can readily show from the result above. Also, the lowest energy possible is not zero, as in the energy “ladders” we have used. The worksheet model is chosen to provide a readily visualized feeling for the entropy concept and direction of change, not quantitative results in this introductory look. |
|||||
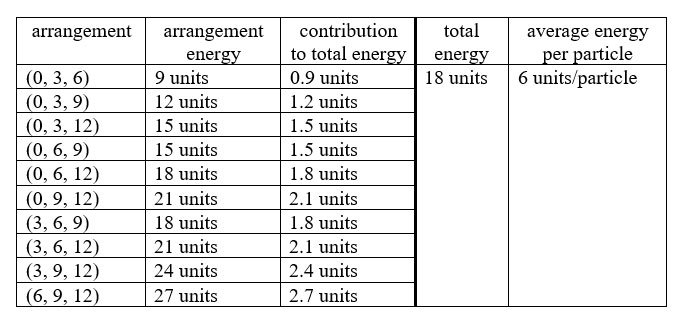
3. |
The ten distinguishable arrangements of a system of three identical particles each of which can have one of five, equally-spaced allowed energies are shown in these diagrams. The table following shows the analysis to find the total energy of the system and the average energy per particle. |
||||
|
|||||
 |
|||||
4. |
There are 10 distinguishable arrangements possible. The first column in the table is constructed to try to show a progressive pattern that will produce all distinguishable arrangements. Identical results for total energy and average energy per particle in this three-particle, five-level system might seem surprising, compared to the three-particle, four-level system. However, under the constraint that the highest energy possible is 12 units, any number of equally-spaced levels (equal to or greater than the number of particles) will give the same result. (Unequally-spaced energy levels, will give different results with the average energy of the particles equal to the average of the energy of the energy levels. For example, energy levels of 0. 2, 6, and 12 units give an average energy per particle of 5 units, the average of the energy levels = 20/4.) |
||||
Part B |
|||||
5. |
Our experience is that gases expand to fill all the space available to them. That is one of the properties we often use to characterize a gas (compared to other phases of matter). Given that there is nothing in the way to prevent movement of particles into the vacuum (after the barrier is removed), this is a process that can happen. The final state is the gas in a larger volume with more closely spaced energy levels (according to the previous paragraphs of the worksheet), which has more distinguishable arrangements possible. Thus, the expanded state is more probable than the compressed state and also explains why gases are never observed to gather themselves spontaneously into a smaller space than is available. |
||||
6. |
We found that the average energy per particle (which is proportional to the temperature of the particles) does not change when equal spacing between energy levels changes within the same range of available energies. This leads to the conclusion that expansion into a vacuum, where nothing changes except the volume available to the particles (which decreases the spacing between energy levels and increases the number of distinguishable arrangements), would not change the temperature of the particles. Indeed, the temperature of a gas does not change when it expands into a vacuum. |
||||
7. |
a) Gas A in the mixture occupies a larger volume than in the separated state, so b) By the same reasoning, WBmix> WB. c) Numbers of distinguishable arrangements in independent parts of a system combine multiplicatively to give the number in the system as a whole, Wseparated = WA× WB. d) Likewise, since the gases act independently in the mixture, e) The results from parts a and b, combined with those from parts c and d, give f) Since Wmixture> Wseparated, the mixture is more probable than the separated gases. That is, if there is nothing to prevent the movement of the particles, gases will spontaneously mix. This is just what we observe for real gases. For example, when you enter a room containing scented flowers, you can detect their scent anywhere in the room. The general principle here is that mixtures are more probable than the separated components. Although the example here is gas mixing, the principle holds for any system where the particles are freely able to move from one place to another, such as liquid mixtures, including solutions. |
||||
Part C |
|||||
8. |
Since Wmixture> Wseparated, the ratio, is greater than unity, so the logarithm of the ratio is positive (> 0). Therefore, |
||||
The general principle embodied here is that entropy change is positive for processes where the final state of the system is more probable (has a higher number of distinguishable energy arrangements) than the initial state. Conversely, if the entropy change for a process is positive, we know that the final state of the system is more probable than the initial state. |
|||||
Part D |
|||||
9. |
For a five-level, three-particle system, which is the result we got previously by counting arrangements. |
||||
10. |
For a nine-level, nine-particle system, This is exactly what is expected, since all levels are occupied by identical particles, there is only one distinguishable way to distribute them. |
||||
11. |
On the solvent side of the barrier, we have nine identical water molecules in nine boxes, so Wsolvent = W9,9 = 1, as we found in the previous item. |
||||
12. |
The solvent and solution sides are independent of one another, so the combined total number of arrangements is Wtotal = Wsolution×Wsolvent = 84 × 1 = 84 |
||||
13. |
|
||||
14. |
|
||||
15. |
The spontaneous change is going to state A, since this is the change for which ΔS > 0. |
||||
16. |
Here is the completed table. |
||||
17. |
Your experience tells you that when a hot and cold object are brought together, the hot one gets cooler, the cold one gets warmer, and, if left together long enough, they come to the same temperature (intermediate between the original hot and cold temperatures). This is what is illustrated in pathway B and is what always happens spontaneously. |
||||
18. |
The data from the previous table are used to complete this table.
Temperature is proportional to the average energy per particle in a system, so the more energy (quanta) one of the four-particle solids has, the higher its temperature. In the first energy transfer, a colder object, (4,2), transfers energy (one quantum) to a hotter object, (4,6). The entropy change for this transfer is negative. The transfer from colder to hotter is not spontaneous, that is, will not occur, as our experience tells us. In the second energy transfer, a hotter object, (4,6), transfers energy (one quantum) to a colder object, (4,2). The entropy change for this transfer is positive. The transfer hotter to colder is spontaneous, that is, will occur, as our experience tells us. In the third energy transfer, a hotter object, (4,6), transfers energy (two quanta) to a colder object, (4,2). The entropy change for this transfer is positive. The transfer is spontaneous, that is, will occur, as our experience tells us. Note that the positive entropy change is even larger than in the previous transfer because the final state (equal temperatures) is more probable than one where there is still a difference in temperature. In the fourth energy transfer, two objects at the same temperature, (4,4), transfer energy (one quantum) so one object get warmer, (4,5) and the other cooler (4,3). The entropy change for this transfer is negative. The net transfer of energy between two objects at the same temperature is not spontaneous, that is, will not occur, as our experience tells us. |
||||
Part E |
|||||
19. |
a) Again, use the data from the (N,n) table, item 16, to get these entropy changes. The entropy change for system A is larger (more positive). b) The entropy change for system A is larger (more negative). c) System A is cooler (lower temperature) than system B, since it always has fewer energy quanta. The transfer of the same amount of energy (one quantum) has a larger entropy effect in a cooler (lower temperature) compared to an identical warmer (higher temperature) object. |
||||
Appendix |
|||||
The “concentrations” on the two sides of the barrier are Cleft = 6/30 = 0.20 Cright = 5/20 = 0.25 |
|||||
Filling the table gives |
|||||
• |
Since the number of distinguishable arrangements for the system increases when a water molecule moves from left to right, this is a spontaneous process. The opposite movement produces a decrease in arrangements and would not occur. |
||||
• |
Osmosis occurs in a direction to make the solution concentrations on each side of the membrane the same, that is, water moves from the less concentrated to the more concentrated to equalize the concentrations. Note that the concentrations come closer together for the spontaneous process (water left to right) and further apart for the non-spontaneous process (water right to left). |
||||
 |
|||||
To obtain a Word file of this Activity, please fill out this brief form to help us track what is happening to our Workbook. We also encourage you to get in touch if you have an activity or idea for an activity that might add to the Workbook. We want to make this an alive and active document. |
|||||
| Back to Table of Contents | |||||
 |