Background

Changes in physical systems, like a solid salt dissolving in water or exchanges between the species complexing the metal ion in a solution of metal complexes, always involve energy and entropy changes. Energy may be required, for example, to break bonds between molecules (or be released when bonds are formed). At the molecular level, entropy is a measure of the number of ways the energy of a system can be distributed among the molecules—the more ways, the more probable the system. Changes occur in the direction toward more probable systems, that is, in the direction of increasing entropy.

For a certain amount of energy in a given molecular system, the number of ways to distribute the energy depends on the freedom of motion of the molecules. In the solid, the molecules (or atoms or ions) are held in place in the solid structure, so their motions are limited and the entropy is low. In the gas, the molecules are far apart and free to move anywhere in their container and the entropy is high. The liquid phase is an intermediate case with an intermediate entropy. The molecules are close together but not held in one place, and able to move about within the constraints of the attractions between them.

Mixtures of two or more different kinds of molecules multiply the number of possible energy arrangements, compared to a system of identical molecules. This is because the same amount of energy can be apportioned in many different ways among the different kinds of molecules.

Important background for this Activity is familiarity with this relationship among entropy change, energy change, and temperature:

(This relationship was introduced and rationalized for countable systems in the Direction of change and entropy Activity. You may have learned about it another way, which is fine.)  The sign of ΔS and ΔE is the same for a system where gain or loss of energy is the only change. And the entropy change is inversely proportional to the Kelvin temperature of the system. This relationship is usually expressed in terms of enthalpy change, ΔH, instead of ΔE, but for changes in condensed phases—solids and liquids—ΔH and ΔE are essentially the same.

Further generalization of entropy analyses

We begin by defining how reacting/changing systems can interact with their surroundings. For the countable systems used to explore the relationship of entropy, energy, and temperature, energy was added to the system with no other change. That was an example of a closed system that can exchange energy, but not matter, with the surroundings. Observable examples of closed systems are the reaction mixtures in Part A below where energy can be readily transferred into or out of the plastic bags. If those reactions were carried out in an insulated container, like an expanded foam cup, no energy would be transferred between the reaction mixture and its surroundings. These would be examples of isolated systems that can exchange neither energy nor matter with the surroundings. (Open systems can exchange both energy and matter with the surroundings. We will examine no open systems.)

The diagram to the right is designed to aid our further discussions. This closed system can exchange thermal energy (heat, no work) with the thermal surroundings. The thermal surroundings are assumed to have a very large heat capacity, so they maintain a constant temperature as they gain energy from or transfer energy to the system. If a change in the system is exothermic, the system transfers this thermal energy to the thermal surroundings, which undergoes an equivalent endothermic change. That is, the energy (enthalpy) changes are equal and opposite in sign.

          ΔH_syst = – ΔH_surr

To analyze a change in the system, the net entropy change—system plus thermal surroundings— has to be determined.

          ΔS_net = ΔS_syst + ΔS_surr

The only change in the thermal surroundings is loss or gain of thermal energy, so we can use the energy-temperature-entropy relationship.

Substituting – ΔH_syst for ΔH_surr gives

This equation is the basis for determining whether a change in an isolated or closed (limited to thermal energy exchange) system is spontaneous—has a positive ΔS_net. (How fast it may occur is irrelevant.) The power of this equation is that the net entropy change (the entropy change of the universe) can be determined from system parameters without explicitly considering the surroundings. Thus,

          ΔS_net> 0,  system change is spontaneous
          ΔS_net< 0,  system change is non-spontaneous
          ΔS_net = 0,  system is at equilibrium

We have introduced the concept of equilibrium, a system “in balance” that has no tendency to change in either the forward or reverse direction. Under the given conditions for the system, its entropy is at maximum, as large as it can be (energy distributed in as many ways as are possible). Note that use of the energy-temperature-entropy relationship to analyze phase changes assumes ΔS_net = 0 (without making it explicit). If a phase change is at equilibrium and left to itself—no interaction with its surroundings—the amounts of the two phases remains unchanged.

With this understanding of system and surroundings, we can answer the question: if gases have higher entropies, why do condensed phases exist? For a spontaneous solid to liquid (melting), liquid to gas (vaporization), or solid to gas (sublimation) phase change to occur, its ΔS_net must be positive.

All of these changes require an input of energy, that is, ΔH_syst must be positive. Thus,
            ,
the contribution of energy change to ΔS_net, is negative, so the contribution of ΔS_syst must be positive, in order that ΔS_net > 0. ΔS_syst is, of course, positive for all these changes.

But at low enough temperature, the negative term,
           
(which effectively represents the entropy change in the surroundings), overwhelms the positive change in the system’s entropy change. Thus, which phase of a substance predominates is a function of temperature—condensed at low temperature and gas at higher temperature. You have likely observed examples of this, such as ice cubes that remain solid in the freezer but become liquid at room temperature or a pan of boiling liquid water on the hot stove with a cloud of condensed water droplets in the cooler air above the pan.

The equation for ΔS_net may look a bit familiar to some, but likely not in terms of ΔS_net. Multiply through by –T to get

          – TΔS_net = – TΔS_syst + ΔH_syst

For reasons that are not relevant here, a new variable, the Gibbs free energy, ΔG_syst, is defined as

          ΔG_syst ≡ – TΔS_net = – TΔS_syst + ΔH_syst

Although Gibbs free energy is very useful in analyzing many chemical and biological processes, it can be confusing. What is often confusing about this new variable is that negative values characterize spontaneity. That’s why a focus on the entirely equivalent ΔS_net generally “feels” like it makes a good deal of sense and how we will proceed in this Activity. We’ll first use ΔS_net to analyze solubility (both dissolution and precipitation, two sides of the same coin).

A. Reaction energies and entropies

The energy involved in a reaction can often be detected by touching the reacting system or its container. This works because your skin is sensitive to the gain or loss of energy (which your brain interprets—on the basis of experience—as temperature change). To describe the energy of a reaction, we sometimes write the energy as a reactant or product.

            exothermic reaction                chemical reactants → chemical products + energy
            endothermic reaction              chemical reactants + energy → chemical products

1.

If an endothermic reaction takes place in a test tube you are holding in your hand, will you feel it getting cooler or warmer? Explain your reasoning clearly.

Here, you will use this technique to determine the signs of reaction energy changes as solid salts dissolve in water.

•

DISPOSAL: When you have completed all the observations you wish with this system, discard the solutions down the drain with plenty of running water.

2.

Write a reaction expression, including energy, that describes what happens when solid calcium chloride, CaCl₂, is mixed with water. Explain clearly and as completely as possible the evidence that leads you to write this expression.

3.

Write a reaction expression, including energy, that describes what happens when solid ammonium nitrate, NH₄NO₃, is mixed with water. Explain clearly and as completely as possible the evidence that leads you to write this expression.

4.

What do your observations allow you to conclude about the sign of ΔS_net for the reaction when CaCl₂ is mixed with water?

5.

What do your observations allow you to conclude about the sign of ΔS_net for the reaction when NH₄NO₃ is mixed with water?

6.

Does either of the energy level diagrams in Figure 1 represent the dissolution reaction of CaCl₂ in water? Does either diagram represent the dissolution reaction of NH₄NO₃ in water? Explain the reasoning for your responses.

7.

What conclusion(s), if any, can you draw about ΔS_syst for the dissolution of calcium chloride in water? Clearly explain your reasoning.

8.

What conclusion(s), if any, can you draw about ΔS_syst for the dissolution of ammonium nitrate in water? Clearly explain your reasoning.

Calcium carbonate, CaCO₃, the major component of chalk, limestone, and marble [and a central player in Earth’s carbon cycle (see Part D), including ocean chemistry, biology, and geology], is an insoluble salt. Its very limited solubility varies with temperature, as shown in this plot.

9.

Is the dissolution of calcium carbonate endothermic or exothermic? [Consider LeChatelier’s principle: a reaction at equilibrium will react to a stress (such as being heated) in a way to reduce the stress (shift in the direction that uses up the added energy). How will the direction of equilibrium shift as temperature is increased, if energy is a “reactant”? a “product”?] Is ΔH_syst positive or negative? Which energy level diagram in Figure 1, A or B, represents the dissolution of calcium carbonate? Explain the rationale (based on the solubility plot evidence) for your responses.

10.

What conclusion(s) can you draw about ΔS_syst for the dissolution of calcium carbonate in water? Clearly explain your reasoning. Can you think of a molecular level explanation that could explain the sign of ΔS_syst? (What might be the effect of ionic charge on the freedom of motion of surrounding water molecules?)

Tables of standard enthalpies of formation, ΔH⁰_f (from their elements at one atmosphere pressure and 298 K), and standard entropies, S⁰, are available for a large number of elements, compounds, and ions. The values in the following table are for the species in the reactions just discussed, including aqueous dissolution of calcium carbonate (in its aragonite crystalline form most prevalent in seawater).

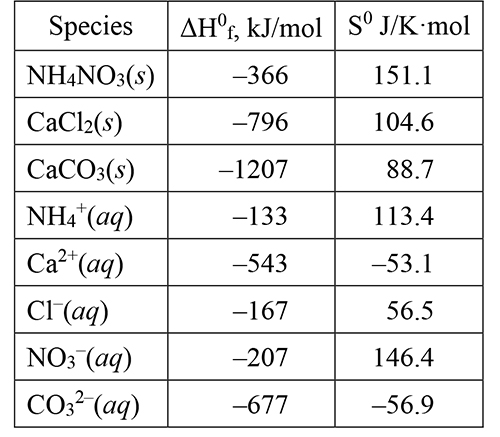The standard enthalpy change for a reaction, ΔH⁰_rxn, is the algebraic sum of the standard enthalpies of formation for the products minus the algebraic sum of the standard enthalpies of formation of the reactants: ΔH⁰_rxn = ΣΔH⁰_f(product) – ΣΔH⁰_f(reactant). The sums have to account for the stoichiometry of the reaction, that is, the number of moles of each reactant and product. The standard entropy change for a reaction, ΔS⁰_rxn, is found in the same way. (These are examples of the way thermodynamic quantities can be combined to give values for changes of interest.)

11.

Use these values to calculate the ΔH⁰_rxn and ΔS⁰_rxn (= ΔH⁰_syst and ΔS⁰_syst) for the dissolution of ammonium nitrate, calcium chloride, and calcium carbonate in water. Are the results consistent with the signs (positive or negative) you assigned to ΔH_syst and ΔS_syst in the previous items? Explain your response.

12.

Use the values for ΔH⁰_syst and ΔS⁰_syst found in the previous item to calculate the standard net entropy change, ΔS⁰_net (in J/K·mol at 298 K) for the dissolution of ammonium nitrate, calcium chloride, and calcium carbonate in water. Are these values for ΔS⁰_net consistent with your observations for these reactions? Explain why or why not.

The standard entropy of atoms, elements, and compounds is always positive and, in principle, can be obtained directly without reference to any other substance. Ions in aqueous solution are a different story. There is no way to make measurements of the properties of “isolated” anions or cations in solution because an ion must always be present together with ions of the opposite charge. This requires that some ion be chosen as a reference, to which all others are compared. The reference chosen is the aquated hydrogen cation, H⁺(aq) or H₃O⁺(aq), assigned a value zero J/K·mol at 298 K. Depending on how their interactions with the surrounding water molecules compare to the hydrogen cation, the entropies of aquated ions may be positive or negative. You can see this in the small table above.

13.

Which ions in the table have a positive S⁰? Which ions have a negative S⁰? What property, if any, do the ions with a positive S⁰ have in common? What property, if any, do the ions with a negative S⁰ have in common? Based on this very limited sample of ions, what molecular level interaction(s) might explain your observations?

Solubility and insolubility are explored further in the forthcoming Solubility patterns Activity.

B. Temperature and direction of change

The sign of ΔS⁰_net is determined by the signs and relative magnitudes of its ΔS⁰_syst factor (entropy change within the system) and its
          
factor (equivalent to an entropy change in the thermal surroundings). For some changes, both factors go in the same direction, but, for others, they go in opposite directions. Sometimes you find changes described as “entropy driven” (where the ΔS⁰_syst factor determines the direction of change) or “energy driven” (where the
          
factor determines the direction of change). Both of these are misleading. Entropy does not “drive” anything. Only energy can bring about a change or movement. Entropy may be thought of as directing how the energy gets distributed. This is like a person giving directions who points the way, but does not actually participate in getting there. The apparent energy factor is really an entropy factor,
          ,
in determining the direction of change.

14.

The contribution of the thermal entropy factor,
          ,
to the net entropy change is always positive for an exothermic reaction. The only way the reaction can be unfavorable (net entropy change negative) is for the system entropy change to be negative and large enough to overwhelm the exothermicity. Which (if any) of the reactions in items 11 and 12 fall into this category? Given your previous thinking about these reactions, was this surprising or expected? Explain.

15.

The contribution of the thermal entropy factor to the net entropy change is always negative for an endothermic reaction. The only way the reaction can be favorable (net entropy change positive) is for the system entropy change to be positive and large enough to overwhelm the endothermicity. Which (if any) of the reactions in items 11 and 12 fall into this category? Given your previous thinking about these reactions, was this surprising or expected? Explain. (Note that the thermal entropy factor is dependent on temperature and will be less negative, if the reaction can be carried out at a higher temperature.)

C. Entropy and equilibrium

In the analyses above, reactions were treated as “go” or “no go”. The ionic salts were either soluble or insoluble (of such limited solubility as to be treated as insoluble). In these cases, the sign of the standard net entropy change, ΔS⁰_net, calculated from standard entropies and standard enthalpies of formation, indicated whether the change was spontaneous or not (soluble or insoluble, for example). However, there are many reactions that are not “go”/ “no go”, but come to a balance of forward and reverse reaction with a significant amount of both reactants and products still in the reaction mixture. This is an equilibrium mixture that is characterized by both the sign and magnitude of its standard net entropy change, ΔS⁰_net. Examining the effect of temperature on a colorful, easily characterized, equilibrium system will help to understand the relationship of net entropy and equilibrium.

Procedure, questions, and analyses

In crystals and solutions, cobalt(II) ions form many colorful complexes whose colors depend on the number and identity of the species complexed with the ion and their geometry around the ion. Some complexes with six species arranged octahedrally around the ion are generally deep pink or magenta. Other complexes, with four species arranged tetrahedrally around the ion, are usually blue. Two examples of complex ions in aqueous solution are represented here.

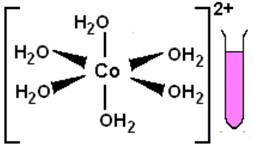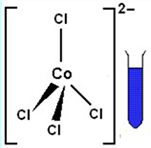16.

What conclusion(s) might you draw about the number and geometry of species complexed around the cobalt(II) ion in the aqueous Co(H₂O)₆Cl₂, solution? What is the evidence for your response?

17.

What conclusion(s) might you draw about the number and geometry of species complexed around the cobalt(II) ion in the alcoholic Co(H₂O)₆Cl₂, solution? What is the evidence for your response?

•

Put on safety glasses or goggles. Use the plastic pipet to add 1 or 2 drops of the aqueous solution to the alcoholic solution and swirl the alcoholic solution to make sure it is thoroughly mixed. Continue repeating this process, being sure to mix thoroughly between additions of the aqueous solution, until the mixed solution becomes a lavender color—a combination of pink and blue cobalt(II) complexes.

Evidence from studies of cobalt(II) solutions suggests that this solution might be characterized by this equilibrium reaction:

All species are solvated by the water-alcohol mixture denoted by solv. Both the pink and blue complexes are visible (to give the lavender color) in this room temperature solution, so the equilibrium between them can be represented by this equilibrium ratio of concentrations:

Although, the actual concentrations of the two complexes are not known, the equal font size of the words in the brackets is meant as a reminder that both are detectable at room temperature.

•

Divide the lavender solution about equally among the three test tubes. Prepare an ice-water bath in one of the plastic cups. Use the available hot water to prepare a hot-water bath in another of the cups. The baths should be deep enough so the liquid in the test tubes will be totally immersed when the tube is in the bath.

•

WARNING: Water at 50 °C will not cause burns, but is very uncomfortable on the skin (and some find it painful). Take care to avoid touching the hot water or splashing it on yourself or others.

•

Place one of the test tubes of lavender solution in the ice-water bath and another in the hot-water bath. Place the third in the empty cup to retain as a control to make any changes caused by the lower and higher temperatures easy to observe. Leave the test tubes in the low and high temperature baths for 5-10 minutes to be sure the solutions have reached the bath temperatures. Record any changes you observe.

18.

What, if any, change(s) did you observe in the solution cooled to low temperature? If there was a change, is it reversible? What could you do to find out? Do it.

19.

What, if any, change(s) did you observe in the solution heated to high temperature? If there was a change, is it reversible? What could you do to find out? Do it.

•

DISPOSAL: When you have completed all the investigations you wish with this system, pour the aqueous and alcoholic solutions into the labeled collection containers provided.

The observed color changes of the lavender solution, as the temperature is changed, can be interpreted to provide an important relationship between entropy and equilibrium. We will outline the analysis for the room to low temperature change and then you can extend it to the room to high temperature change. As the solution cools it changes from lavender to more pink. The equilibrium is shifting toward the reactant and the low temperature equilibrium ratio of the complex concentrations can be written as:

The relative sizes of the fonts is a reminder that the concentration of the pink complex has increased and the concentration of the blue complex has decreased. The comparison between the magnitude of the equilibrium ratios at room and low temperatures is

            K_room  > K_low

Now, we need to see how the standard net entropy changes compare for the low and room temperature reactions. A very useful assumption is that the standard system enthalpy change, ΔH⁰_syst, and standard system entropy change, ΔS⁰_syst, for a reaction are constant, independent of temperature. This is often quite a good assumption, if the temperature change is not more than a few tens of degrees. With this assumption, the standard net entropy changes are:

To compare these standard net entropy changes, take their difference:

Cooling the solution, that is, removing energy (enthalpy), drives the reaction written above in reverse. This means the change from blue complex to pink complex is exothermic—energy is leaving the system. Conversely, the reaction as written, pink complex to blue complex, must be endothermic—the system’s energy (enthalpy) change must be positive, ΔH⁰_syst. Therefore, because T_low< T_room:

and

Since the difference between these net standard entropy changes is positive (greater than zero), we know that ΔS⁰_{net room} is more positive than ΔS⁰_{net low}. Note carefully that this does not tell us whether the actual values of these net standard entropy changes are positive or negative. Both could be negative, as long as ΔS⁰_{net room} is less negative than ΔS⁰_{net low}. (What this amounts to is that more positive is the same as less negative.) Keeping in mind that we are expressing relative positiveness, the relationship between these net standard entropy changes is:

Comparing this relationship of the net standard entropy changes to the relationship between the previous equilibrium ratios for the reaction, K_room> K_low, shows that the more positive entropy change is associated with the larger equilibrium ratio. A more positive entropy change means the change is more favorable. That is, the reaction products are more favored at room temperature than at low temperature. This is what the larger equilibrium ratio for the room temperature reaction also indicates. Now, it’s up to you to see whether this correlation of net standard entropy change with equilibrium ratio holds for the high temperature.

20.

Write the equilibrium ratio expression for K_high, modeled on those written above for the room and low temperature cases. Clearly explain the evidence for your expression and how it compares with K_room.

21.

Carry out the analysis, clearly explaining each step, to find the relationship between
ΔS⁰_{net room} and ΔS⁰_{net high}. Do your results (items 20 and 21) reinforce the correlation of net standard entropy changes with equilibrium ratios we found above? Explain your response.

Generalizing from a single example, like the cobalt(II) system here, is not always a wise idea, but the same kind of correlation among temperature, equilibrium ratios, and net standard entropy changes is found for all reactions. This must mean that there is a causal relationship, not simply a correlation, among these variables. Let K_eq be the value of the equilibrium ratio expression with the concentrations of all the relevant reactants and products accounted for at a particular temperature. If ΔS⁰_net is the net standard entropy change for the reaction at this temperature, the relationship between equilibrium and entropy is (where R is the gas constant, 8.314 J/mol·K):

            ΔS⁰_net  =  R·lnK_eq

D. Carbon cycles

Life on Earth is carbon-based, that is, based on molecules with carbon-containing structures. There is also carbon in inanimate materials. In fact, there is at least 250 times as much carbon in Earth’s rocks (its lithosphere) than in its atmosphere, biosphere, and oceans combined. Carbon is always on the move among all these reservoirs. Some of the changes occur in seconds and others take many millennia, but all involve increase in net entropy. Since the total amount of carbon does not change, there must be cycles of change that carbon atoms undergo and returns them to the state where they started. Here we will examine a very slow and a very rapid cycle.

Rock weathering and metamorphism

The reactions of interest here are:

At first sight, the weathering sum and metamorphic reactions look like the simple reverse of one another, but that is far from the truth. Each is the initial and final state of a complicated series of reactions that involve quite different conditions and intermediates. Weathering takes place at the Earth’s surface at close to standard pressure and temperature and requires the presence of water. The metamorphic transition from carbonate rock to silicate rock occurs deep within the Earth at high pressure and temperature under anhydrous conditions. With the data in this table, we can learn more from their energy, entropy, and temperature relationships.

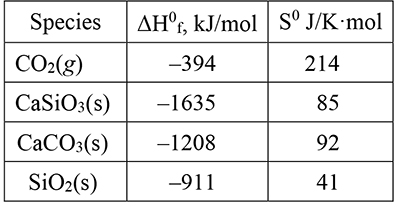22.

Weathering occurs under close to standard conditions, one atmosphere pressure and 298 K. What are ΔH⁰_syst and ΔS⁰_syst for the weathering reaction? Show that weathering is a spontaneous process under these conditions. Explain clearly the reasoning you use to draw this conclusion.

Weathering is an important process for removing carbon dioxide from the atmosphere. The products are moved by streams and rivers to the sea, where they sink to the bottom. Over many millennia, the products end up deep within the crust and subducted into the mantle. Weathering is a spontaneous change, but that does not mean it is a rapid change. The Antarctic ice-core data in Figure 3 can help estimate the rate of the weathering process.

For at least the past million years, and probably longer, the Earth has been relatively cold with thick ice sheets covering the top third of the northern hemisphere. This extended ice age has been interrupted about every 100,000 years by interglacial warm periods (like the one we are in now) lasting a few thousand years before slowly growing cold again.

The warming periods begin when the orbit and tilt of the planet position it to receive a little more solar energy that melts some of the ice sheet and raises the temperature a bit. The warming sea releases carbon dioxide to the atmosphere, since the gas is less soluble at higher temperature. The addition of the carbon dioxide increases the greenhouse effect and reinforces the warming. And more warming further increases the release of dissolved carbon dioxide leading to more warming. This positive feedback loop is evident in the close tracking of the temperature and carbon dioxide concentration shown in Figure 3. In tandem with the rise of carbon dioxide, the warmer climate causes more water to evaporate and adds the greenhouse effect of water vapor. Transient changes in the planetary orbit and tilt can only initiate the interglacial periods. They are sustained and strengthened by the carbon dioxide and water vapor feedback greenhouse effect.

23.

As the ice sheets melt, land and seas are exposed to sunlight. What, if any, effect might this have on planetary temperature? Explain the reasoning and any evidence for your response.

Warming comes to a stop when the carbon dioxide concentration reaches about 280 parts per million (ppm) in the atmosphere. Annual cyclic changes among air, land, and sea carbon-containing compounds (see below) are balanced and maintain a constant atmospheric carbon dioxide concentration within a few ppm. There is no longer a net increase of atmospheric carbon dioxide. At this point, the very slow process of weathering can make itself felt as it removes atmospheric carbon dioxide (as carbonate) and buries it at the bottom of the sea.

24.

What, approximately (within about ten percent), is the difference in ppm of the atmospheric carbon dioxide at its minimum and maximum over the past 400,000 years? Clearly explain the evidence and reasoning for your response.

25.

On average (within about ten percent), how long did it take for the atmospheric carbon dioxide to drop from its maxima to its minima during the past 400,000 years? Clearly explain the evidence and reasoning for your response.

26.

What was the average rate of loss (ppm per millennium) of atmospheric carbon dioxide from its maxima to its minima during the past 400,000 years? Show your reasoning and evidence clearly.

27.

In a little over 200 years since the Industrial Revolution, human activities have added about 135 ppm of carbon dioxide to the atmosphere. If we stopped adding this extra greenhouse gas immediately, how many years do you estimate it would take natural processes to return the atmosphere to its pre-Industrial Revolution level of carbon dioxide? Is this worrisome? Why or why not? Present the reasoning for your responses clearly.

Since ΔS⁰_net for the weathering reaction sum is positive (spontaneous), ΔS⁰_net for the “reverse” metamorphic change at standard conditions would be negative (non-spontaneous).

28.

We would expect the change in the standard system entropy, ΔS⁰_syst, for the metamorphic process to be positive (as it is). Explain why this is expected.

29.

Why is the change in standard net entropy, ΔS⁰_net, for the metamorphic process negative? Consider the information in Part B, item 15. Is there a clue there for a way to make the net entropy change for the metamorphic process less negative? Explain clearly.

30.

Assume that the changes in system enthalpy, ΔH⁰_syst, and entropy, ΔS⁰_syst, for the metamorphic process are constant, independent of temperature. (This is a huge approximation, but, in the absence of better data, such approximations are sometimes useful to provide directional reasoning.) At what temperature would the net entropy change, ΔS⁰_net, for the metamorphic process be zero? Clearly explain your reasoning and procedure.

31.

The temperature of the Earth’s magma ranges from about 1000 to 1600 K. Why does it make sense that the weathering products subducted into the magma undergo the metamorphic process spontaneously? Clearly explain your reasoning.

When volcanos erupt, magma reaches the surface of the Earth and metamorphic carbon dioxide gas is released to the atmosphere. Magma close to the surface, generally in the vicinity of volcanos, can also release its carbon dioxide through cracks in the crust, as shown in Figure 4. The carbon dioxide in the streams of bubbles coming through vents in the sea floor is released to the atmosphere. The carbon in this gas is thus returned to the atmosphere from which it came millions of years before. It is likely that every atom of carbon on Earth has been part of a carbonate rock at least once during the 4.5 billion year life of the planet.

Photosynthesis and respiration

Essentially all the carbon in our food, fuel, fabrics, organic building materials (wood and plastic) and in organisms came originally from carbon dioxide in the atmosphere or dissolved in the seas. The first steps in capturing this carbon is photosynthesis in green plants, algae, and phytoplankton. A representation of the photosynthetic process is:

The oxidation and reduction reactions are written in this way to make it easier to account for the electrons. There are, of course, no free electrons, e^-, or protons, H⁺, in the system and the CH₂O product simply represents the empirical formula of a carbohydrate. The large number of steps and enzymes and other biomolecules involved in this oxidation-reduction process are not shown. (The “dark” reaction does not have to take place in the dark, but has this name because the reaction does not require light.) The overall photosynthetic reaction is conventionally written as (where C₆H₁₂O₆ is the carbohydrate glucose):

           6 CO₂(g) + 6 H₂O(l) + 6 light → C₆H₁₂O₆(s) + 6 O₂(g)

32.

Photosynthesis takes place at the surface of the Earth under close to standard conditions of temperature and pressure. Use the data in this table to calculate ΔH⁰_syst for the reaction of the chemical species in this process. Would ΔH⁰_syst provide a positive or negative contribution to the spontaneity of the process? Explain why or why not. Since life, as we know it, depends on photosynthesis, how would the process overcome any barrier caused by ΔH⁰_syst? Clearly explain your response.

33.

Calculate ΔS⁰_syst for the reaction of the chemical species in the photosynthetic process. Could you have predicted the sign of ΔS⁰_syst without doing a calculation? Explain clearly how you might do this.

34.

Calculate ΔS⁰_net for the reaction of the chemical species in the photosynthetic process. Up to now, the source of energy for endothermic reactions has been assumed to be a reservoir that transfers thermal energy to the system, with its contribution to the net entropy change given by
.
But photosynthesis is not driven by thermal energy transfer, but by the energy in light, so the entropy change in the light source has to be accounted for in the net entropy change. Does it make sense that the entropy change (energy dispersal/spread) in the light source, the Sun, compensates for net entropy calculated here? Explain how this might be.

Molecular oxygen, O₂(g), is a reactive gas that has not always existed free on Earth. Figure 5 is an estimated timeline for the evolution of atmospheric oxygen gas. These estimates are based mainly on isotopic analyses of  materials in Earth’s crust.

For the first 1.5 billion years of the Earth’s existence (until about three billion years ago), its oxygen atoms were present mainly in carbon dioxide, water, and carbonate and silicate rocks. About 2.9 billion years ago, cyanobacteria near the surface of the sea evolved the photosynthetic water oxidation reaction and began to produce molecular oxygen. (There is uncertainty about the time cyanobacteria evolved, so this time is noted with a question mark in Figure 5.) For the previous billion years, life had depended on other reducing agents, like sulfides and iron, to provide the electrons necessary to reduce carbon dioxide in the dark reaction. A few organisms that actually live in the dark, such as those at the bottom of the oceans, still use these reducing agents.

The molecular oxygen first produced reacted quickly with dissolved reductants (sulfides and iron) and organic matter (organisms). It was about half a billion years before enough of these reductants had been oxidized for molecular oxygen to begin to escape to the atmosphere. This appearance of molecular oxygen in the atmosphere about 2.4 billion years ago is called the Great Oxygenation Event (stage 2 beginning). Reactions with reductants on land limited the build-up of atmospheric molecular oxygen to only about 10% as much as at present. The presence of this easily available oxidant for respiratory energy production (see below) supported the evolution of more complex single-celled organisms and ultimately multicellular organisms (during stage 3) and the evolution of plants and animals on land (stage 5).

Finally, plants evolved in the sea about 800 million years ago and atmospheric oxygen levels began to climb toward present-day levels (stage 4). Plant cells contain special structures called chloroplasts that are the locations for the photosynthetic oxidation of water. Their ancestors are photosynthetic cyanobacteria that were engulfed at some point by a larger organism that gained an evolutionary advantage by having this internal source of electrons (and protons) for carbon dioxide reduction. It’s likely that all organisms that are photosynthetic owe this capability to an ancient cyanobacterium.

Respiration is the process organisms use to produce the energy they need to sustain their lives. Fundamentally, at the cellular level, respiration involves returning electrons from reduced carbon-containing (organic) molecules to molecular oxygen from the atmosphere (or dissolved in the sea). A major pathway for respiration is (the “reverse” of photosynthesis):

          C₆H₁₂O₆(s) + 6 O₂(g) → 6 CO₂(g) + 6 H₂O(l)

Note that this is, effectively, the combustion reaction for glucose. But, instead of a rapid reaction releasing thermal energy and light, this respiration process occurs in many steps, at about ambient temperature. The energy released is “captured” by synthesizing adenosine triphosphate, ATP, molecules, the energy currency for organisms. Other organic molecules, amino acids and fatty acids, are also used as electron sources in respiration. Since the reduced carbons in these molecules were derived from glucose, writing the respiration reaction this way makes sense for keeping track of electrons in the overall oxidation-reduction reactions of photosynthesis and respiration.

35.

What are ΔH⁰_syst, ΔS⁰_syst, and ΔS⁰_net for the respiration reaction? Do the signs and magnitudes of these variables make sense for this “combustion” reaction? Explain clearly the reasoning for your response.

Since the respiration reaction occurs in a series of steps, the large enthalpy and entropy changes you just found occur in small positive amounts (that add up to the total) at each step. At several of these steps the process that occurs also results in the synthesis of an ATP molecule from ADP, adenosine diphosphate, and inorganic phosphate, P_i (schematic reaction expression):

            ADP + P_i → ATP

The thermodynamics of this reaction, under biological conditions, are a bit difficult to determine, but a reasonable value is ΔS⁰_net ≈ –111 J/K·mol. The reaction is unfavorable (it is both endothermic, strong bonds are broken and weaker bonds are formed and two reactant species become a single product species), but it can proceed if it is part of an overall process that has a positive net entropy change. That is what happens at the steps along the respiration pathway where ATP is produced.

36.

Experiments show that about 32 ATP molecules are produced per glucose oxidized by respiration. The overall process can be characterized by this reaction expression:

            C₆H₁₂O₆(s) + 6 O₂(g) + 32 ADP + 32 P_i → 6 CO₂(g) + 6 H₂O(l) + 32 ATP

What is ΔS⁰_net for this overall process? Explain your reasoning clearly.

Carbon dioxide is captured from the atmosphere by photosynthesis and returned to the atmosphere by respiration of all aerobic organisms. There are sources and sinks for CO₂ on Earth’s surface (including the seas). A growing tree turns large amounts of CO₂ into glucose, uses some of it in respiration to stay alive and grow, and uses a great deal of it to create its new, larger structure. As long as the tree stays alive the carbon in its structure does not re-enter the atmosphere, so the tree is a sink for CO₂. It removes more than it returns to the atmosphere. If the tree dies, it no longer removes CO₂ from the atmosphere, but the organisms that cause its decay (fungi and bacteria, for example) use the organic matter in the wood as food, so their respiration returns the carbon to the atmosphere. The decaying tree is a net source of CO₂. Whether a forest is a net sink or source for atmospheric CO₂, therefore, depends largely on the balance between photosynthesis by the living plants and respiration in the decaying organic matter of dead plants.

In weathering and metamorphism, the cycle of carbon from carbon dioxide to carbonates and back to the atmosphere as carbon dioxide takes millions of years. The cycle of carbon from the atmosphere to land and sea and back through photosynthesis and respiration is a faster process.

37.

Data you can use to develop an understanding of the time scale of carbon cycling among the atmosphere, land, and sea are available in Figures 6, 7, 8, and 9. The figures focus on atmospheric carbon dioxide at different time scales. Construct an explanatory narrative (a “story”) that ties together all four figures in terms of the timing of this carbon cycle. It is useful to know that one part per million of carbon dioxide in the atmosphere is eight gigatonnes (eight billion metric tons) of carbon dioxide.

38.

During the second decade of the 21st century, human-caused emissions of CO₂ have been about 40 gigatonnes per year, the great majority of which come from burning fossil fuels. What do the previous four graphs tell you about the fate of this CO₂? Over the short term (a few years), what part of the photosynthesis-respiration cycle would you expect the added CO₂ to affect more? Is there evidence for this in the graphical data? If the human emissions stop, what has to happen for the greenhouse effect to come to a steady state (solar energy in equal planet energy out) and the temperature of the Earth to stop rising? Clearly explain your reasoning and the evidence you use.

Instructor/presenter notes

This Activity is designed to follow the Direction of change and entropy Activity which introduces a molecular-level, countable-systems model for entropy. The fundamental messages were that entropy is a measure of the number of ways that energy can be distributed in a system and that spontaneous change occurs in a direction to maximize entropy. The model was applied to mixing, osmosis, and freezing point depression and used to rationalize the relationship among entropy change, energy change, and temperature,
          

Part A

For each group, prepare two zip-seal plastic sandwich bags, one containing one teaspoon of granular anhydrous solid calcium chloride, CaCl₂(s), and the other one teaspoon of granular solid ammonium nitrate, NH₄NO₃(s). Seal the bags and use a felt-tip marker to label them appropriately as "CaCl₂" and "NH₄NO₃". Be sure there is a source of room temperature water, so a heating or cooling effect when mixing with the solids is easy and obvious to detect. The amount of water used in each bag should be about 60 mL (about 2 ounces). The directions are written assuming 4-ounce cups. Alter, if necessary, to fit what you use.

DISPOSAL: The solutions can be poured down the drain with plenty of running water to flush them through the trap.

The first eight items on the worksheet are “scaffolded” to reach the conclusions about the signs of the entropy changes for the dissolutions. There are a variety of single-use hot and cold packs commercially available, but we have chosen to use the baggie-and-water-cup systems here, so they are the “same”—a white solid dissolving in water.

1.

An endothermic reaction takes in energy from its surroundings, including your hand holding the test tube where the reaction occurs. Since energy is removed from your hand, your brain interprets this as a decrease in temperature. You feel the test tube and contents getting cooler.

2.

When CaCl₂(s) dissolves in water, the solution feels warmer (even, perhaps, hot). Energy enters your hand and leaves the reaction, so we can write the reaction as:

            CaCl₂(s) → Ca²⁺(aq) + 2 Cl^-(aq) + energy

3.

When NH4NO3(s) dissolves in water, the solution feels cooler. Energy leaves your hand and enters the reaction, so we can write the reaction as:

            NH₄NO₃(s) + energy → NH_4⁺(aq) + NO₃^-(aq)

4.

The dissolution of CaCl₂(s) in water occurs readily when the two components are mixed. The reaction is spontaneous. The reaction occurs in the direction written above, so ΔS_net > 0 (is positive).

5.

The dissolution of NH₄NO₃(s) in water occurs readily when the two components are mixed. The reaction is spontaneous. The reaction occurs in the direction written above, so ΔS_net > 0 (is positive).

6.

The dissolution of CaCl₂(s) in water is exothermic, and corresponds to diagram A in Figure 1. More energy is released when the ions are solvated than is required to dissociate the solid into its constituent ions.

The take-home message here is that there are both exothermic and endothermic spontaneous reactions (reactions that occur without requiring any external forcing). That is, reactions for which ΔS_net is positive. The contribution of energy to ΔS_net is
.
The next two items examine what the experimental observations and their implications tell us about ΔS_syst for these reactions.

7.

A negative ΔH_syst, for an exothermic reaction, gives a positive contribution to ΔS_net, and always tends to make the reaction spontaneous. If the magnitude of ΔS_syst for this reaction is negative and large enough, it might overwhelm the energy contribution and make the reaction non-spontaneous. In the case of CaCl₂(s) dissolution, we cannot tell the sign of ΔS_syst, because it could be positive (adding to the effect of the negative ΔH_syst) or negative (but not large enough to swamp the effect of the negative ΔH_syst).

8.

A positive ΔH_syst, for an endothermic reaction, gives a negative contribution to ΔS_net, and always tends to make the reaction non-spontaneous. The only way the reaction can be spontaneous is for ΔS_syst for the reaction to be positive and large enough to overwhelm the negative energy contribution. In the case of spontaneous endothermic NH₄NO₃(s) dissolution, we can conclude that ΔS_syst is positive and large enough to swamp the effect of the positive ΔH_syst.

9.

The very limited solubility of CaCO₃ decreases as the temperature increases. This is consistent, by LeChatelier’s principle, with the dissolution being exothermic.

            CaCO₃(s) → Ca²⁺(aq) + CO_3^2-(aq) + energy

Energetically, this corresponds to the energy level diagram labeled A in Figure 1.

10.

CaCO₃(s) is very sparingly soluble, that is, its dissolution is not spontaneous. ΔS_net for the dissolution is negative. Since ΔH_syst for the dissolution is negative (exothermic), the enthalpy contribution to ΔS_net,
,
is positive. Therefore, we can conclude that ΔS_syst is negative and large enough to swamp the positive effect of ΔH_syst. Since the dissolution is energetically favorable and mixing (mixing the ions with water to make the solution) always increases entropy, something must be going on in the solution that decreases its entropy. A clue is in the exothermicity of the dissolution. Evidently, there are strong interactions among the water molecules and the dissolving ions that release more energy than is required to separate the ions from the crystal. If the interactions tie up a lot of water molecules (by attractions to the multiply-charged ions) and decrease their ability to move about as usual, the energy levels available in the solution will be decreased. This will decrease the number of ways energy can be distributed in the solution and lower its entropy. This idea is explored further in the forthcoming Solubility patterns Activity.

Introducing standard enthalpies of formation, ΔH⁰_f (from their elements at one atmosphere pressure and 298 K), standard entropies, S⁰, and their numerical values is a break from the previous work in this entropy Activity as well as the previous Direction of change and entropy Activity. Up to now, reasoning was mainly directional and qualitative. The introduction of numerical values and calculations is a change that may need more attention and instruction than the very brief paragraph (really just a reminder) in this Activity. It is your decision how much background you need to provide on these topics for your curriculum and to familiarize students with the calculations of reaction thermodynamics that follow in this Activity.

11.

NH₄NO₃(s) → NH_4⁺(aq) + NO_3^-(aq)

            ΔH⁰_syst = (–133 kJ/mol) + (–207 kJ/mol) – (–366 kJ/mol) = 26 kJ/mol
            ΔS⁰_syst = (113.4 J/K·mol) + (146.4 J/K·mol) – (151.1 J/K·mol) = 108.7 J/K·mol

We observed (experimentally) this dissolution to be endothermic and ΔH⁰_syst is positive, thus endothermic. We reasoned that ΔS⁰_syst should be positive, since ΔS_net is positive (reaction is spontaneous), and ΔS⁰_syst is positive.

CaCl₂(s) → Ca²⁺(aq) + 2 Cl^_-(aq)

            ΔH⁰_syst = (–543 kJ/mol) + 2 (–167 kJ/mol) – (–796 kJ/mol) = –81 kJ/mol
            ΔS⁰_syst = (–53.1 J/K·mol) + 2 (56.5 J/K·mol) – (104.6 J/K·mol) = –44.7 J/K·mol

We observed this dissolution to be exothermic and ΔH⁰_syst is negative, thus exothermic. We could not assign a sign to ΔS⁰_syst, except to reason that, if it is negative, it can’t be negative enough to overwhelm the enthalpy effect. ΔS⁰_syst is negative and in the next item, we will find the relative contributions of enthalpy and entropy to ΔS⁰_net.

CaCO₃(s) → Ca²⁺(aq) + CO₃^2-(aq)

           ΔH⁰_syst = (–543 kJ/mol) + (–677 kJ/mol) – (–1207 kJ/mol) = –13 kJ/mol
           ΔS⁰_syst = (–53.1 J/K·mol) + (–56.9 J/K·mol) – (88.7 J/K·mol) = –198.7 J/K·mol

12.

NH₄NO₃(s) → NH_4⁺(aq) + NO_3^-(aq)

We observed this dissolution to be spontaneous and ΔS⁰_net is positive, thus spontaneous.

CaCl₂(s) → Ca²⁺(aq) + 2 Cl^-(aq)

We observed this dissolution to be spontaneous and ΔS⁰_net is positive, thus spontaneous.

CaCO₃(s) → Ca²⁺(aq) + CO₃^2-(aq)

13.

The ions in the table with positive S⁰ are NH_4⁺, Cl^-, and NO₃^-. Those with negative S⁰ are Ca²⁺and CO₃^2-. The ions with positive S⁰ all are singly charged (1+ or 1–), while those with negative S⁰ are both multiply charged (2+ and 2–). In item 10 above, it was suggested that reducing the freedom of motion of the water molecules in the hydration layer around the more highly charged ions reduced the energy levels available to the water and thus reduced the entropy, making it unfavorable for these ions to be in solution.

Part B

14.

The limited dissolution of CaCO₃(s) is exothermic, but the entropy change for the system is negative and large enough to overwhelm the exothermic effect. It can seem surprising to find that a reaction that “runs downhill” (that is, gives off energy) proceeds to such a small extent. This is why it is important to understand the role of entropy as the directionality factor. (Note that the dissolution of CaCl₂(s) also falls into the category of negative ΔH⁰_syst and negative ΔS⁰_syst, but, in this case, the thermal entropy term dominates and the reaction proceeds readily.)

15.

The dissolution of NH₄NO₃(s) is endothermic, but the entropy change for the system is positive and large enough to overwhelm the endothermic effect. It can seem surprising to find that a reaction that “runs uphill” (that is, requires energy) should readily proceed. This is why it is important to understand the role of entropy as the directionality factor.

Part C

The experiment that starts this part is simple and colorful, but with one “tricky” step. Care has to be taken in making the lavender solution mixture, as it is easy to pass the lavender point, if mixing between additions of the aqueous solution is not thorough. Vigorous swirling (without splashing) between additions should be emphasized—using an Erlenmeyer flask facilitates this mixing. Cobalt(II) chloride hexahydrate dissolves relatively slowly in the alcohol; crushing the solid to a fine powder will speed the dissolution. (Be careful to use 99% isopropanol rubbing alcohol, not the more common 70% or 93%, which will not work. Pure 2-propanol is OK, as well, but more expensive and unnecessary.) Note that the aqueous, alcoholic, and mixed solutions all have the same concentration of cobalt and chloride ions, but differ in the ratio of water to alcohol. If a group overshoots the lavender point by a couple drops, you can provide them a bit of the alcoholic solution to try to recover the appropriate solvent ratio. Making hot (≈50 °C) water available in a container with a handle or an electric kettle will make it easy for each group to prepare their hot water bath.

DISPOSAL: Solutions of cobalt salts should not be disposed down the drain. Remaining aqueous solution can be collected and saved to do this or another experiment later or the water evaporated and solid salt recovered to be reused, as indicated here for the alcoholic solutions. Alcoholic solutions can be collected and the solvent evaporated over a steam bath (or moderate temperature hot plate) in a hood. The solid remaining after evaporation can be crushed and used to prepare aqueous or alcoholic solutions for this or another experiment, with the caveat that the solid will likely contain some trapped solvent.

16.

The aqueous CoCl₂·6H₂O, solution is pink, which suggests that there are six species complexed in an octahedral array around the cobalt(II) ion. The formula of the compound is very suggestive that the complexing species are water molecules. Since the vast number of other species in the aqueous solution are also water molecules, it further makes sense that water is doing the complexing. But, see below for further discussion of cobalt complexes.

17.

The alcoholic CoCl₂·6H₂O, solution is blue, which suggests that there may be four species complexed in a tetrahedral array around the cobalt(II) ion. It’s possible that reducing the number of water molecules in the solution has made it less probable for six water molecules to complex the cobalt(II) ion. It’s also likely that chloride ions are among the complexing species and that charge and/or size factors are responsible for changing the number and kind of complexing species in this solution.

The correlation of structure and color of cobalt(ii) complexes is not as simple as we have said so far. The colors of the complexes are due to their absorption of light energy in the visible region of the spectrum. The energy transitions responsible for the absorptions are for electrons in the ion’s 3d orbitals. If there were a uniform electric field around the ion, the five 3d orbitals would all have the same energy. In a non-uniform electric field, such as caused by complexing species surrounding the ion, the orbitals do not all have the same energy. An electron in a lower energy orbital can absorb energy from some visible wavelength of light to transition to a higher energy orbital. That wavelength of light is lost and we see only the colors that are left.

The wavelength that is absorbed depends on how far apart the non-uniform electric field has split the energies of the 3d orbitals. Water molecules produce a relatively strong field and cause a fairly large split of the orbital energies. Complexing with water causes the absorption of energy at the high energy, blue, end of the spectrum, leaving the red and giving a pink complex. Chloride ions produce a weaker non-uniform electric field and, therefore, a smaller energy split of the orbital energies. Complexing with more chlorides causes the absorption of energy at the low energy, red, end of the spectrum, leaving the blue and giving blue complexes.

The relative abundances shown in the figure are temperature sensitive. The complexes with more chlorides (the blue ones) become more abundant as the temperature increases. Advantage was taken of this temperature dependence of the color to develop an experiment to determine the temperature effect on the equilibrium between the CoCl(H₂O)₅⁺ and CoCl₂(H₂O)₂ complexes, Koga, N., Kimizu, T., Sakamoto, M., Furukawa, Y., “Temperature Effect on Cobalt(II)-Chloride Complex Equilibrium in Aqueous Solution”, Chem. Educator 2009, 14, 225–228. The conditions for this quantitative investigation are much like those at the 5-molal HCl concentration in the figure. Although the blue complex is lower in concentration than the pink in this region, the blue color is much more intense (higher absorbance). Not too much shift in the concentration ratio is necessary to change from a pink to blue solution.

A quick, qualitative investigation, modeled on this aqueous HCl solution of cobalt(II) ion, would provide the same conceptual analysis as the Activity here. We have chosen the alcohol-based system because it poses none of the safely hazards of a relatively concentrated HCl solution. The alcoholic solution may provide the appropriate ratio of water to chloride ion activities to mimic the aqueous HCl solution at the balance point between the monochloro and dichloro complexes, CoCl(H₂O)_5⁺ and CoCl₂(H₂O)₂, respectively. Also, the higher dielectric constant of the mixed solutions should favor the charged, monochloro complex, so more of it is formed at the same temperature in the mixed solvent. Any ambiguity about the exact species present is circumvented by focusing just on the colors in making the analyses.

Cobalt(II) in aqueous solutions with a high concentration of NaCl also shows the pink-to-blue change as temperature is increased but are not “lavender-enough” at room temperature to make the changes as obvious as in the alcoholic solution. Also, the salt solution lacks the pedagogical value of being able to produce a lavender solution by mixing pink and blue solutions, thus emphasizing that it contains both complexes.

18.

When the lavender solution is cooled in the ice bath, the solution becomes pink. To test reversibility, let the pink solution warm back to room temperature to see if it returns to lavender or transfer it to the high temperature bath to see if it turns blue. [Be sure students actually test these solutions to prove for themselves that the reaction is reversible.]

19.

When the lavender solution is heated in the high temperature bath, the solution becomes blue. To test reversibility, let the blue solution cool back to room temperature to see if it returns to lavender or transfer it to the ice water bath to see if it turns pink.

20.

Since the solution is blue at the high temperature, the reaction must have formed more of the blue complex at the expense of the pink. The equilibrium ratio that that reflects this is:
           

Compared to the equilibrium ratio for the room temperature solution, K_room, the numerator is larger and the denominator is smaller, so the ratio is larger, that is,

            K_high> K_room

21.

Analysis of the relationship between ΔS⁰_{net room} and ΔS⁰_{net high} follows the same pattern as for the room to lower temperature, with appropriate changes to account for the direction of change, increasing temperature. Assume that the standard system enthalpy change, ΔH⁰_syst, and standard system entropy change, ΔS⁰_syst, for the reaction are constant, so the standard net entropy changes are:

To compare these standard net entropy changes, take their difference:

Warming the solution, that is, adding energy (enthalpy), drives the reaction (pink to blue) in the direction it is written. This means the change from pink complex to blue complex is endothermic—energy is added to the system—the system’s energy (enthalpy) change must be positive, ΔH⁰_syst > 0. Therefore. because T_high> T_room:

           
and

Since the difference between these net standard entropy changes is positive (greater than zero), we know that ΔS⁰_{net high} is more positive than ΔS⁰_{net room}. Reiterate that this does not tell us whether the actual values of these net standard entropy changes are positive or negative. Both could be negative, as long as ΔS⁰_{net high} is less negative than ΔS⁰_{net room}. It is worth a simple example (or reference to a number line, preferably one that is vertical instead of horizontal). Consider the case that the numerical values for ΔS⁰_{net high} and ΔS⁰_{net room} are  –4 and –10, respectively. Then, ΔS⁰_{net high}– ΔS⁰_{net room} = (–4) – (–10) = +6, a positive difference. Keeping in mind that we are expressing relative positiveness, the relationship between these net standard entropy changes is:

Comparing this relationship of the net standard entropy changes to the relationship between the previous equilibrium ratios for the reaction, K_high > K_room, shows that the more positive entropy change is associated with the larger equilibrium ratio. A more positive entropy change means the change is more favorable. That is, the reaction products are more favored at high temperature than at room temperature. This is what the larger equilibrium ratio for the high temperature reaction also indicates. The correlation of net standard entropy change with equilibrium ratio holds for the range of temperatures studied in this Activity:

            ΔS⁰_{net high} > ΔS⁰_{net room} > ΔS⁰_{net low}

            K_high > K_room > K_low

Introduction of the quantitative relationship between standard net entropy changes and equilibrium ratios is not necessary, if it is not relevant for your curriculum. You can delete this material from the worksheet. This applies as well to the free energy content in this material.

Part D

Rock weathering and metamorphism
The reaction, Ca²⁺(aq) + 2 HCO₃^-(aq) → CaCO₃(s) + CO₂(g) + H₂O(l), the part of weathering that occurs in the sea, is explored in Carbon dioxide’s ocean chemistry, especially as related to human-caused increase in atmospheric carbon dioxide. If you were to use that Activity as well as this one, the various possible fates of the CaCO3(s) formed in this reaction should be discussed.

22.

To determine whether or not the overall weathering process is spontaneous under standard conditions, the standard net entropy change for the reaction is needed and can be calculated from the standard entropy and enthalpy changes for the system (the reaction).
                                   
    ΔH⁰_syst = [ΔH⁰_f(CaCO₃)  + ΔH⁰_f(SiO₂)] – [ΔH⁰_f(CaSiO₃)  + ΔH⁰_f(CO₂)]
    ΔH⁰_syst = [(–1208 kJ/mol)  + (–911 kJ/mol)] – [(–1635 kJ/mol)  + (–394 kJ/mol))]
    ΔH⁰_syst = [–2119 kJ/mol] – [–2029 kJ/mol] = –90 kJ/mol = –90x10_³ J/mol
    ΔS⁰_syst = [S⁰CaCO₃)  + S⁰(SiO₂)] – [S⁰(CaSiO₃)  + S⁰(CO₂)]
    ΔS⁰_syst = [(92 J/K·mol)  + (41 J/K·mol)] – [(85 J/K·mol)  + (214 J/K·mol)]
    ΔS⁰_syst = [133 J/K·mol] – [299 J/K·mol] = –66 J/K·mol
   
The positive ΔS⁰_net indicates that the overall weathering reaction is spontaneous under standard conditions. Although the system entropy change, ΔS⁰_syst, is negative (because the large number of energy distributions associated with a gas, the carbon dioxide, are lost in the reaction), the substantial exothermicity, system enthalpy change, compensates to give the positive net entropy change. This enthalpy contribution to the net entropy change depends on temperature and we will see the consequences below.

23.

On warm, sunny days people generally wear white or light color clothing to reflect away sunlight, because they know from experience that darker clothing absorbs more energy and makes them feel warmer. The Earth works the same way. Snow and ice are good reflectors of sunlight, as you know, if you have been “blinded” by light reflected from a snowy landscape on a bright sunny day. If the snow and ice melt, the sunlight is no longer reflected, but is absorbed by the darker land and especially water, which is an excellent absorber of sunlight. Absorption of more sunlight means there is more energy added to the Earth, which contributes further to its warming.

24.

The minima in the blue, carbon dioxide, curve in Figure 3, seem to be consistently a little less than 190 ppm, so a reasonable estimate for a minimum is 185 ppm. There is some more variation in the maxima with a variation from about 280 to 295 ppm, with three of the four below 290, so 285 ppm should be a reasonable estimate and well within a 10% spread of values. Thus, the difference between the maximum and minimum carbon dioxide concentrations is about 100 ppm (=285 – 185 ppm).

25.

The times required to drop from maximum to minimum carbon dioxide concentrations were about 65000 years (=325000 – 260000 years), 70000 years (=240000 – 170000 years), and  70000 years (=135000 – 65000 years). The average of these values, 68000 years, is within the 10%, spread of the values and is an estimate for the time required for the maximum carbon dioxide concentrations to reach their minimum.

26.

A millennium is 1000 years. The result from item 25 shows that it takes 68 millennia for 100 ppm carbon dioxide (item 24) to be removed from the atmosphere, mainly by weathering.

27.

Rate is amount per time. In this case, the rate is known (item 26) and the amount is 135 ppm. The time required is amount divided by rate (the rate expression rearranged).

This result shows that the present level of climate disruption (weather extremes, more destructive wildfires, ocean acidification, and more) will continue far into the future if only natural processes are available to remove the carbon dioxide we have added to the atmosphere. Not only do we have to stop adding more carbon dioxide to the climate system, we have to develop ways to remove what we already put there.

28.

The metamorphic process, CaCO₃(s) + SiO₂(s) → CaSiO₃(s) + CO₂(g), produces a gas, with its large number of energy distributions contributing to the entropy of the products and hence a positive contribution to the net entropy change.

29.

The positive contribution to the standard net entropy change from the system entropy change (item 28) is overwhelmed, under standard conditions, by the endothermicity of the reaction, ΔH⁰_syst > 0, and its negative contribution to net entropy change,
           .
This negative contribution to the net entropy change depends on the temperature and gets smaller as the temperature increases. This means it might be possible for the metamorphic process to be spontaneous, if the temperature was high enough (and the enthalpy not too different) for the negative enthalpy contribution to net entropy to become smaller than the positive system entropy change.

30.

Assuming that ΔH⁰_syst and ΔS⁰_syst are constant, the task here is to find a temperature, T, such that ΔS⁰_net is zero. At any higher temperature, it would be positive, ΔS⁰_net > 0, and the reaction would be spontaneous. Begin by setting ΔS⁰_net = 0,

          ,
rearranging,

          ,

and solving for T, substituting numerical values for ΔH⁰_syst and ΔS⁰_syst (signs reversed form item 22),

Where, if at all, is this high temperature available on the planet?

31.

Assuming our characterization of the metamorphic process and the temperature for its transition to a spontaneous process (item 30) are reasonably correct, temperatures in the magma are sufficient (greater than about 1360 K) to make the process spontaneous. Above about 1630 K, the negative enthalpy contribution to the net entropy change is overwhelmed by the positive system entropy change, that is, ΔS⁰_net > 0 and the reaction is spontaneous. Figure 4 provides evidence for the metamorphic process from magma not far below the sea bed producing carbon dioxide that escapes into the sea and rises to be released into the atmosphere (from whence it could have come millions of years before).

Photosynthesis and respiration

The photosynthetic process is not conventionally represented as two half reactions, but is shown in that form here to make explicit that it is an oxidation-reduction reaction. The light-driven oxidation of water (which produced and continues to produce our atmospheric oxygen) yields the reducing power (shown as electrons) that reduces carbon dioxide carbon from its +4 oxidation state to its 0 (zero) oxidation state. The redox nature of the reaction as well as its separation into two physically distinct parts (the light and dark reactions) gets lost in the conventional reaction,

           6 CO₂(g) + 6 H₂O(l) + 6 light → C₆H₁₂O₆(s) + 6 O₂(g)

32.

Calculate ΔH⁰_syst for the chemical species in the above photosynthetic reaction.

     ΔH⁰_syst = [ΔH⁰_f(C₆H₁₂O₆) + 6 ΔH⁰_f(O₂)] – [6 ΔH⁰_f(CO₂)  + 6 ΔH⁰_f(H₂O)]

     ΔH⁰_syst = [(–1274.4 kJ/mol) + 6 (0 kJ/mol)] – [6 (–393,51 kJ/mol)  + 6 (–285.83 kJ/mol))]

     ΔH⁰_syst = [–1274.4 kJ/mol] – [–4076.04 kJ/mol] = 2801.6 kJ/mol

An endothermic change, ΔH⁰_syst > 0, always makes a negative contribution to ΔS⁰_net for a reaction. In addition to this effect on the net entropy, the large ΔH⁰_syst here represents a high energy barrier, since the reaction occurs at ambient temperature with no source of this much thermal energy. Since the reaction requires light, it’s likely that the energy from light is what helps the reaction overcome the energy barrier.

A deeper look at photosynthesis (that you may choose to take or not, as you assess your curriculum) shows that both red light (600-700 nm range) and blue light (400-500 nm range) are required. Assume that one photon each of red and blue light have to be absorbed to oxidize two water molecules in the initiating photo reaction. For a mole of this reaction (producing a mole of O₂), a mole each of red and blue photons are required. A mole of the red light photons has about 200 kJ of energy and a mole of blue photons about 260 kJ. (The relationship of wavelength and energy is part of the Light energy: absorption, emission, and planetary temperature Activity.)  Thus, for each mole of the photo reaction, 460 kJ of light energy are required. The conventional reaction shown above requires six moles of the photo reaction for each mole of glucose produced, a total of 2760 kJ [= 6 (460 kJ)]. This simple argument suggests that almost all (and perhaps all) of the energy required to overcome the enthalpy barrier is provided by the light absorbed in the photoreaction.

33.

Calculate ΔS⁰_syst for the chemical species in the above photosynthetic reaction.

    ΔS⁰_syst = [S⁰(C₆H₁₂O₆)  + 6 S⁰(O₂)] – [6 S⁰(CO₂)  + 6 S⁰(H₂O)]

    ΔS⁰_syst = [(212.1 J/K·mol)  + 6 (205.14 J/K·mol)] – [6 (213.74 J/K·mol) + 6 (69.91 J/K·mol)]

    ΔS⁰_syst = [1442.94 J/K·mol] – [1701.9 J/K·mol] = –259.0 J/K·mol

This substantial negative system entropy change for the reaction is not surprising and is predictable. The six moles of gas on the reactant and product sides of the reaction pretty much cancel one another out in terms of numbers of possible energy distributions. That means the entropy change is dominated by the comparison between the entropy of six moles of liquid reactant to one mole of solid product. Just in terms of the much larger number of molecules among which to distribute energy on the reactant side, its entropy is going to far outweigh the single mole of product (even though this product is more complex, which increases the possible number of energy distributions—but not nearly enough). The actual entropies confirm this reasoning with the two gases having close to the same value and contributing only about 20% to the change, with the remaining 80% largely from the reduction of six moles to one.

34.

Calculate ΔS⁰_net for the chemical species in the above photosynthetic reaction.

This large negative ΔS⁰_net represents a huge loss in possible energy distributions among the products compared to the reactants, as pointed out qualitatively in the previous item. Since this reaction supports almost all life on Earth, it obviously does occur spontaneously, so there must be some other large positive factor not accounted for in this calculation of ΔS⁰_net. That missing factor is the entropy change associated with the production of the sunlight that drives the photo reaction. The nuclear fusion reactions in the Sun produce an enormous amount of energy that is dispersed into space (the solar system and beyond) in the form of light energy and the kinetic energy of the particles streaming from its surface. The large positive entropy change associated with this exothermicity is the source of the “missing” factor that makes the net entropy change for photosynthesis positive, when all the changes that occur (including those in the Sun) are taken into account.

35.

Chemical species in the respiration reaction, C₆H₁₂O₆(s) + 6 O₂(g) → 6 CO₂(g) + 6 H₂O(l), are identical to the photosynthetic reaction in reverse. The thermodynamic variables are, therefore, the same as calculated in items 32, 33, and 34, but with opposite signs.

      ΔH⁰_syst  =  –2801.6 kJ/mol

      ΔS⁰_syst  =  259.0 J/K·mol

      ΔS⁰_net  =  9660 J/K·mol

36.

To find ΔS⁰_net for the combined reaction of respiration coupled to ATP synthesis, combine the standard net entropy changes for the respiration and synthesis:

      ΔS⁰_{net combo}= ΔS⁰_{net resp} + 32 ΔS⁰_{net synth}

      ΔS⁰_{net combo}= 9660 J/K·mol  +  32 (–111 J/K·mol) =  6108 J/K·mol

The coupled reactions are spontaneous under standard conditions. Under actual cellular conditions the coupled reaction might be less favorable, but still responsible for the energy production of most of life on Earth.

37.

Figure 6 shows that the average concentration of CO₂ in the atmosphere was constant, within about 3 or 4 parts per million (ppm), at 280 ppm for 800 years from 1000 to 1800 AD (now usually abbreviated CE for Common Era). Humans were burning small amounts of fuel for personal use, heating and cooking, but it was almost all biofuel—wood. The carbon in the wood had come from the atmosphere, probably within the previous couple of centuries and was being returned to the atmosphere, so a steady state had been reached with most of the exchange due to natural annual photosynthesis and respiration.

This annual exchange is illustrated in Figure 7, which shows that about 776 gigatonnes of CO₂ are exchanged between the atmosphere and the land and sea each year. This represents about
      
leaving the atmosphere and an equivalent amount being returned. No large swings in the CO₂ concentration are evident in the data in Figure 6 (before 1800). The steady state average is maintained when data are sampled over a few years at a time.

When sampling is done at much shorter intervals, daily, for example, at the observatory on Mauna Loa, Figures 8 and 9, natural annual variations, superimposed on the monotonically increasing CO₂ concentration from human activities, are obvious. The variations are, however, rather small compared to the annual flux represented in Figure 7. For example, in Figure 9, the concentrations at the peaks on May 2020 and May 2021 compared to the concentrations at the pink line on these dates are about 7.5 ppm higher. This is the maximum natural annual variation caused by the changing seasonal imbalance between the amounts of photosynthesis (more in the “summer”, May-September) and respiration (more in the “winter”, October-April). Both processes are occurring all the time, but at rates that depend on the season. But even with this changing balance between removing and adding hundreds of billions of tonnes of CO₂ from and to the atmosphere, the natural imbalance varies by only about 60 billion tonnes [= (7.5 ppm)(8 Gt/ppm)] over the course of a year.

A bit more can be learned about the natural annual variation of the CO₂ concentration by comparing the Mauna Loa data, Figures 8 and 9, with that from the Cape Grim Air Pollution Station in Australia, Figure 11. Mauna Loa is in the northern hemisphere, the location of  the majority of the Earth’s land mass. Cape Grim is in the southern hemisphere, which is largely oceanic. Plants grow and photosynthesize seasonally on land, so there is much more seasonal variation in CO₂ in the northern hemisphere, 7.5 ppm, compared to the southern, about 1.0 ppm. The variation shows up as sort of wiggles on the Cape Grim plot, in contrast to the obvious saw tooth pattern on the Mauna Loa plot. Also note, from Figure 9 and the inset in Figure 11, the reversal of seasons in the two hemispheres. Because of the tilt of the Earth, summer in the north is winter in the south, and vice versa. As a result, the September minimum in CO₂ concentration at Mauna Loa corresponds to the maximum at Cape Grim. The temperatures in the southern hemisphere are moderated (although less so as the planet warms) by the large amount of ocean and the growing season is longer, about half the year compared to about a third in the north.

38.

The pink line in Figure 9 represents the growth of atmospheric CO₂ produced by human activities. It begins at 408.8 ppm on the left axis and ends two years later at 413.0 on the right axis—a growth rate of 2.1 ppm/year or about
      17 Gt/year [= (2.1 ppm/year) (8 Gt/ppm)].
Since humans are producing about 40 Gt of CO₂ per year, there are 23 Gt that are not in the atmosphere, but must be on the land or in the oceans. As an approximation, Figure 7 suggests that land and ocean might each take up about half of this, 12-13 Gt per year, and not return it to the atmosphere that year. In other words, the equal annual flux in each direction shown in Figure 7 is disrupted by the added CO₂ from human activities. About 2-3% more is taken up by the surface than is returned to the atmosphere.

A delay in the return of the CO₂ captured annually on land by photosynthesis makes sense. Some of that CO₂ ends up as part of the plant structure and, for trees, that means it could be many decades or centuries before the tree dies and decays (or its wood is used for something else that ultimately decays). That is, the CO₂ coming annually from respiration includes carbon that was removed from the atmosphere over many years, as well as this year. Figure 6 shows that, before humans started adding CO₂ from carbon that had been captured from the atmosphere millions of years ago, a steady state between photosynthesis and respiration (decay) of organic matter formed over perhaps a century or so. (The chemistry of CO₂ dissolved in the oceans involves more than photosynthesis and respiration and is the topic of Carbon dioxide’s ocean chemistry Activity.)

If human emissions of CO₂ stop (while we still have forests left, but have not developed ways to remove CO₂), there will continue to be an imbalance between photosynthesis and respiration, until respiration/decay can catch up to reach a steady state. With just natural processes, this will take decades (but might be accelerated by the effect of global warming, as the research noted below suggests) and end up with a CO₂ concentration close to what it was when the emissions stopped. That would mean the present climate disruption and climate extremes would be the new “normal” for life on Earth. Unless we develop ways to quickly remove excess human-produced greenhouse gases, this will be an unpleasant future indeed.

The following is text from a 2020 research article: “Rapid Net Carbon Loss From a Whole-Ecosystem Warmed Peatland”.

Plain Language Summary [An abstract written for the non-specialist.]

“Northern bogs and fens have accumulated carbon in deep deposits of peat—dead and decaying plant material high in carbon content—for millennia under wet, cold, and acidic conditions. We experimentally warmed and added CO₂ to a series of bog plots in northern Minnesota to investigate whether warming and drying would lead to the increased decomposition and loss of carbon from bogs to the atmosphere, where it would contribute further to warming. We found that warming changed the nature of these bogs from carbon accumulators to carbon emitters—where carbon was increasingly lost to the atmosphere in the form of greenhouse gases CO₂ and CH₄ as the level of warming increased. This carbon loss was faster than historical rates of carbon accumulation, demonstrating the significant impact of global warming on naturally stored carbon. Improved peatland ecosystem models are capable of capturing the temperature responses but overpredict responses to the elevated CO₂ treatments.”

Hanson, P. J., Griffiths, N. A., Iversen, C. M., Norby, R. J., Sebestyen, S. D., Phillips, J. R., et al. (2020). Rapid net carbon loss from a whole-ecosystem warmed Peatland. AGU Advances, 1, e2020AV000163 (open access)

To obtain a Word file of this Activity, please fill out this brief form to help us track what is happening to our Workbook. We also encourage you to get in touch if you have an activity or idea for an activity that might add to the Workbook. We want to make this an alive and active document.

~ HOME ~