Frequency

Another way to easily produce sound is to suddenly release higher-pressure air into the atmosphere. A balloon is a common way to store a bit of higher-pressure air. When you inflate a balloon, you force air into it, stretching the rubber. The stretched rubber squeezes the air inside, so that the air inside has a higher pressure than the surrounding atmosphere. If you tie off the mouth of the balloon, you have a container of higher-pressure air. If you pierce the sealed balloon with a sharp object, such as a pin, the higher-pressure air is quickly released into the atmosphere. A region of higher-pressure air radiates from where the balloon was and reaches your ears. Then, you hear a pop, something like this.

If you’ve ever played with balloons, you probably know that there is another way to release the air from an inflated balloon. You can do it gradually. Instead of tying the mouth of the balloon shut and breaking the balloon, you can simply let the air out through the its mouth. The higher-pressure air inside the balloon is not released all at once, as when the balloon pops, but over a longer period of time, perhaps several seconds. This release of higher-pressure air also causes variations in the pressure of the air at your ears, and you hear a sound. It sounds like this.

If you’ve played with balloons, you probably also know that you can change the sound by restricting the mouth of the balloon. You can do this by pinching the mouth of the balloon on either side and pulling apart, leaving only a small slit as the opening in mouth of the balloon.

As the air escapes through the slit, it generates a sound with a distinct pitch. Furthermore, the pitch varies with how hard you pull on the balloon. As you pull harder, stretching the balloon more, the pitch goes down. Here is the sound generated by three bursts of air through the stretched mouth of a balloon, with the mouth stretched successively more.

The sound produced by the air escaping through the restricted mouth of a balloon has a definite pitch, unlike the air that escapes from the open mouth. When air escapes through the restricted mouth, it does so as a series of brief pulses. The slit opens and closes rapidly creating these pulses. When the slit is narrow, as it is when the rubber is stretched only slightly, the pulses of air escape rapidly. Rapid pulses of air create rapid fluctuations in pressure, and these produced a high-pitched sound. When the slit is wider, when the rubber is stretched more, the pulses escape more slowly. Slower pulses produce slower pressure fluctuations and a lower-pitched sound.

The relationship between the pitch of a sound the size of an air passage can be observed in other situations, too. The voice of a child has a higher pitch than the voice of an adult. This is the case, because the vocal chords of a child are smaller than the vocal chords of an adult. Vocal chords are membranes that form a slit through which pulses of air from the lungs are emitted. The small slit in the vocal chords of a child produces rapid pulses of air. The larger slit in the vocal chords of an adult produces slower pulses. Rapid pulses produce a higher-pitched sound than slower pulses.

We can visualize the pressure pulses that cause the sensation of sound by making a plot of how pressure varies with time. Practically, such a plot can be made using an electronic device called an oscilloscope. The oscilloscope is capable of displaying how an electrical signal changes in a very short period of time. To see how pressure varies with time, we can use a microphone to translate pressure changes into electrical signals that the oscilloscope can display. When we do this with the first of the three squeals from a balloon, we get the following picture of how pressure varies over a span of 0.01 second.

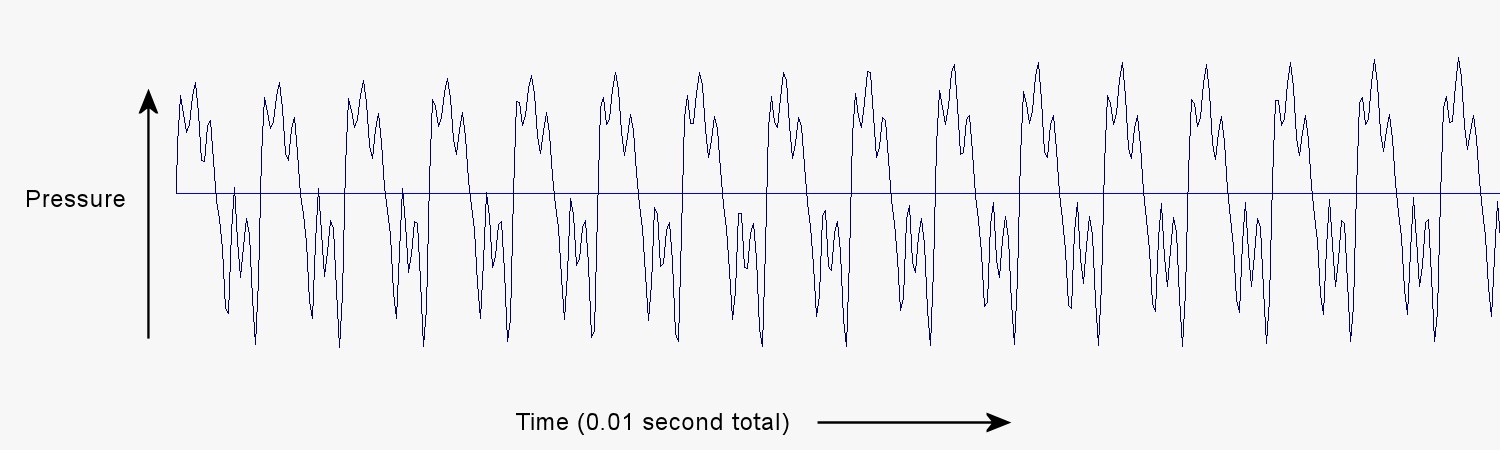
What is immediately striking about this picture is that the pressure variation repeats many times with the same pattern. In other words, the pressure variation is periodic. Over the span of only 0.01 second, the pressure variation repeats a bit over 15 times — about 15.7 times. It repeats 15.7 times in one-hundredth of a second, which is equivalent to 1,570 pulses in one second. This is the frequency of the pressure variation. Frequencies are commonly expressed using a unit called a Hertz, after the German physicist Heinrich Hertz (1857–1894), who made important scientific contributions to the study of electromagnetism. One pulse per second is one Hertz (Hz).

When we make a similar plot of pressure versus time using the second of the three squeals from the balloon, we get the next picture.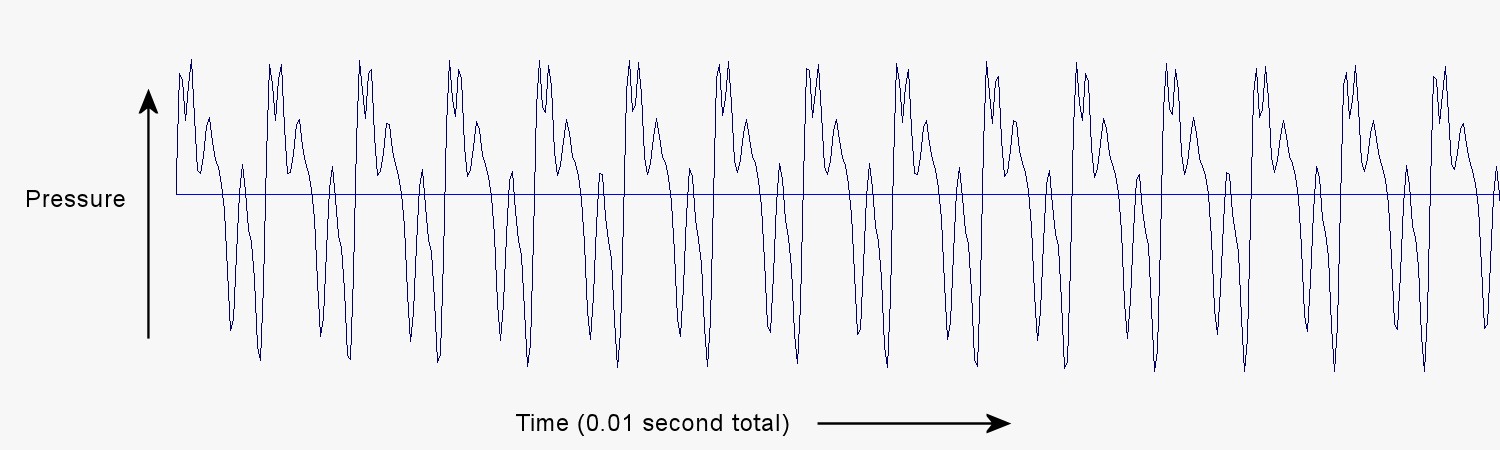

This second picture, like the first, shows that the pressure variation is periodic, although each pulse has a somewhat different shape. It shows another difference, too. The total number of pulses that occur in 0.01 second is a little less than 15, namely 14.8 pulses in 0.01 second. The frequency of the pulses in the second squeal is 1,480 Hz.

We can make a third plot of pressure versus time from the third balloon squeal.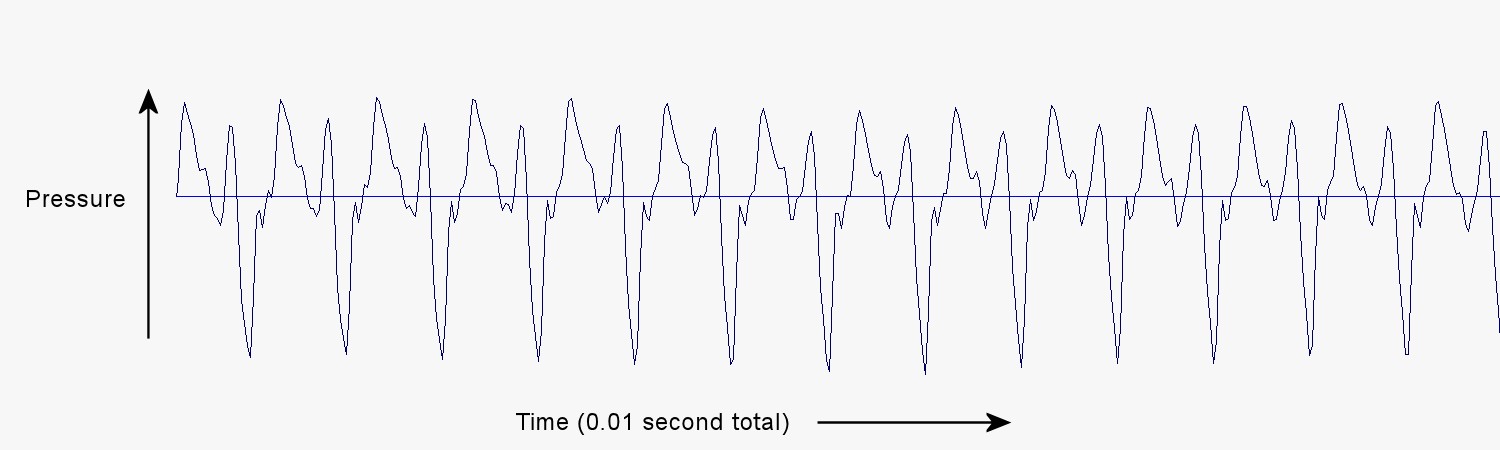

Again, the pressure variation is periodic. The shape of each pulse is different from the shapes of the pulses in both of the previous two plots. The frequency of the pulses is also different. In this case, the total number of pulses in 0.01 second is 13.8, so the frequency is 1,380 Hz.

Listen again to the three squeals from the balloon. The first squeal has a frequency of 1,570 Hz, the second a frequency of 1,480 Hz, and the third a frequency of 1,380 Hz.

When you listen to the three squeals from the balloon, you hear that the pitch of the second is lower than that of the first, and the pitch of the third is lower than that of the second. When you examine the three plots of pressure versus time from the three squeals, you see that the frequency of the pulses decreases from the first to the second to the third, and that the shapes of the pressure pulses differ among the three.  This suggests that the pitch differences you hear may be related to the differences in their frequencies or to the differences in the shapes of the pulses or to both. In order to clarify what factor is significant in determining our sensation of pitch, it helps to compare sounds whose pressure pulses have the same shape. This can be done be comparing sounds that are generated electronically to have pressure pulses of the same shape.

Some synthesized sounds

An electronic synthesizer can produce pressure pulses of various shapes and frequencies. The picture below is a graph of simple pressure pulses generated by an electronic synthesizer at a frequency of 1,570 Hz.

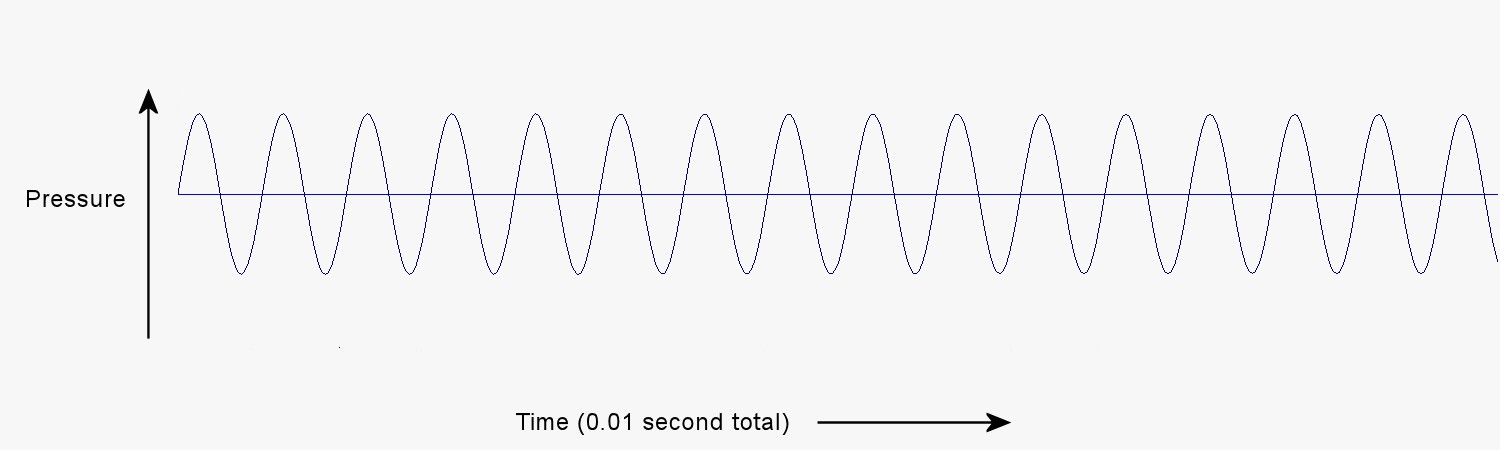
You can hear what these synthesized pressure pulses sound like here:

When the synthesizer produces simple pressure pulses at a frequency of 1,480 Hz, the graph looks like the following picture.

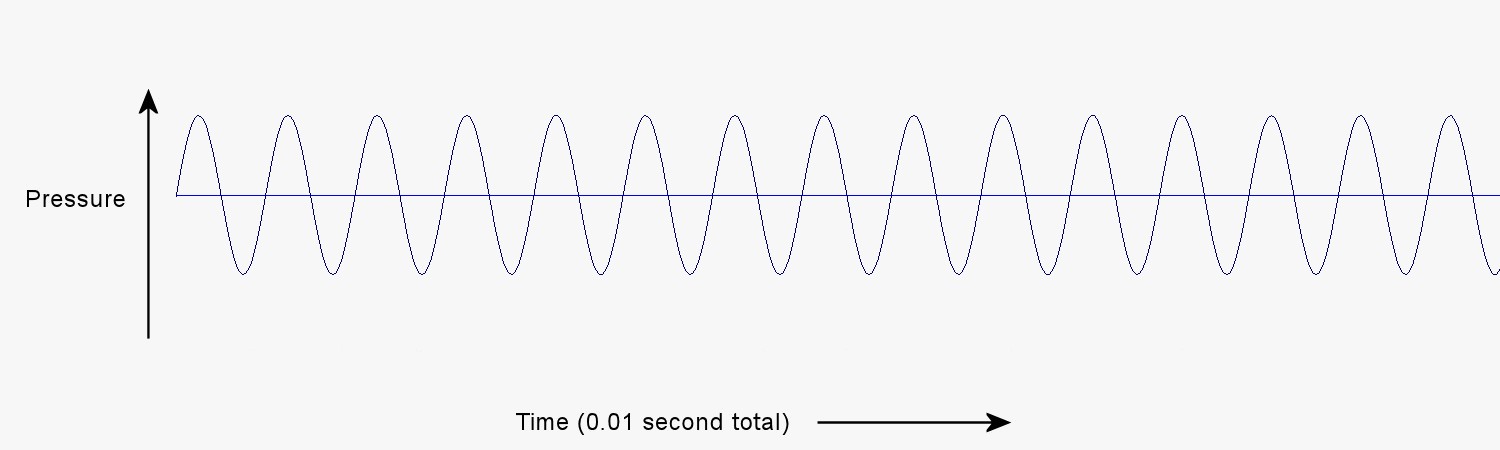
The shape of the pulses are the same as those in the previous graph, but the frequency is higher. You can hear the sound that these pulses produce here:

The sound is very similar to that of the previous example, but the pitch is a bit lower. Next is a graph of simple synthesized pressure pulses at a frequency of 1,380 Hz.

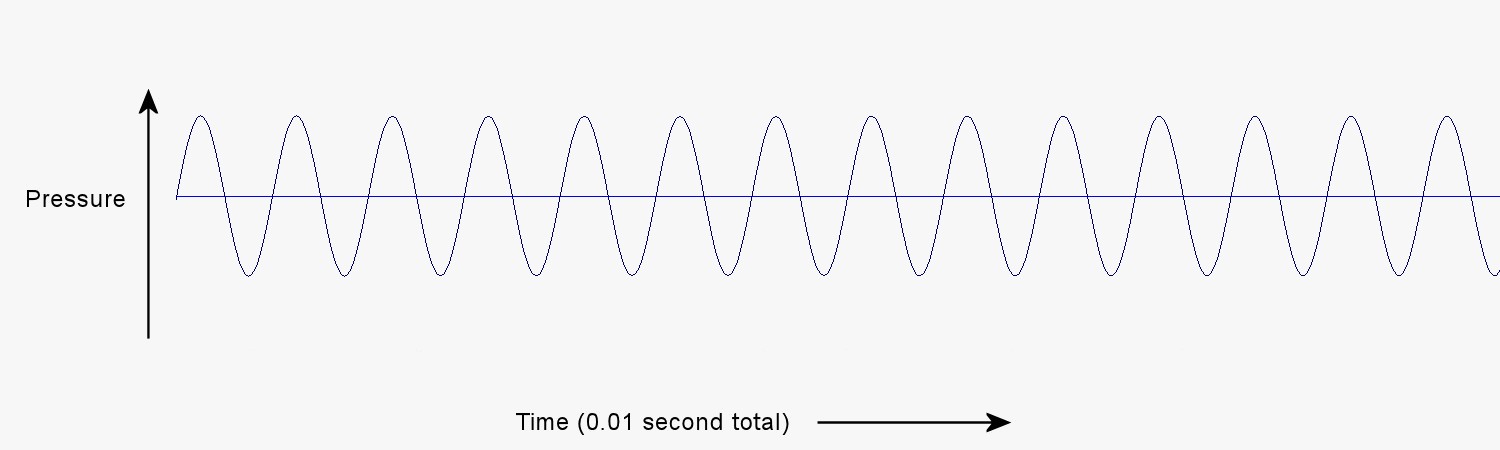
You can hear the sound of these pulses here:

The sound is very similar to the previous two examples, but the pitch is even lower.

In these three synthesized streams of pressure pulses, the pulses all have the same shape. They differ only in the frequency of the pulses. What we perceive is that the sounds produced by these three streams of pressure pulses are very similar, but that they differ in pitch. These three streams of pressure pulses show that the pitch we perceive is related to the frequency of the pulses, not to their shapes. The higher the frequency of the pulses, the higher the pitch we perceive.

What effect does the shape of the pressure pulses have on what we hear? The electronic synthesizer can produce pressure pulses of various shapes. We can see several different pulse shapes in the graphs below, and listen to the sounds those shapes produce. All of the pulses have the same frequency, namely 1,380 Hz.

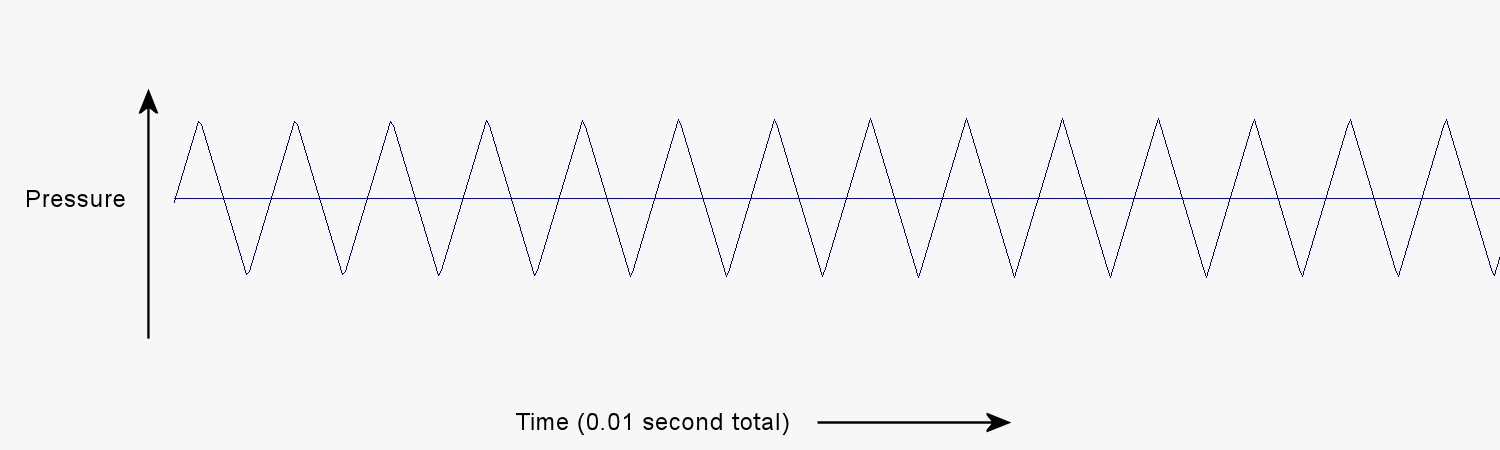
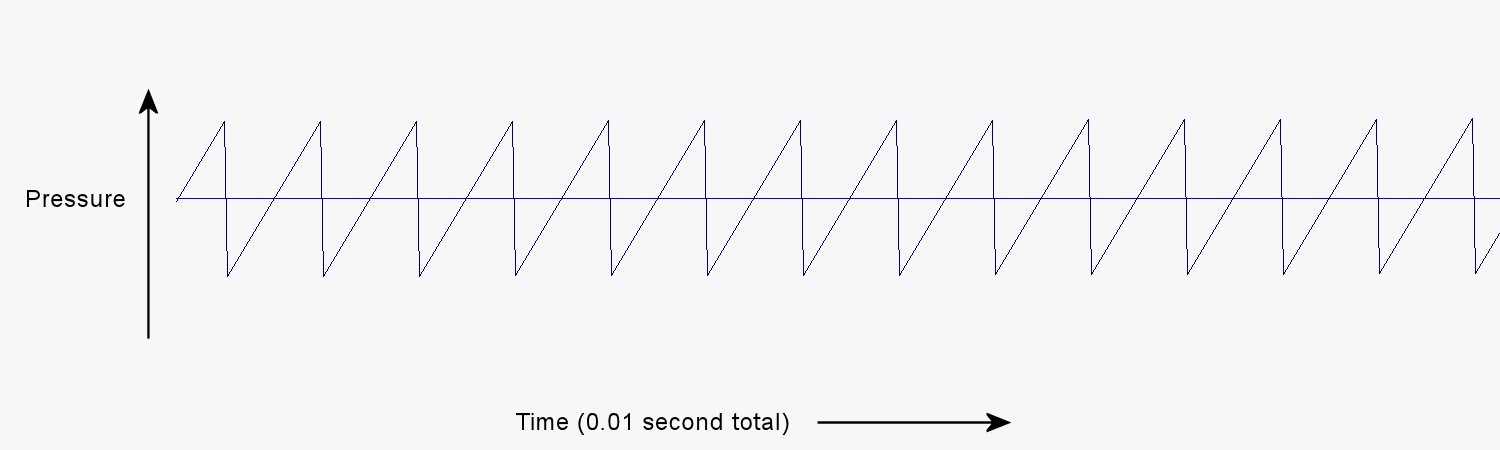
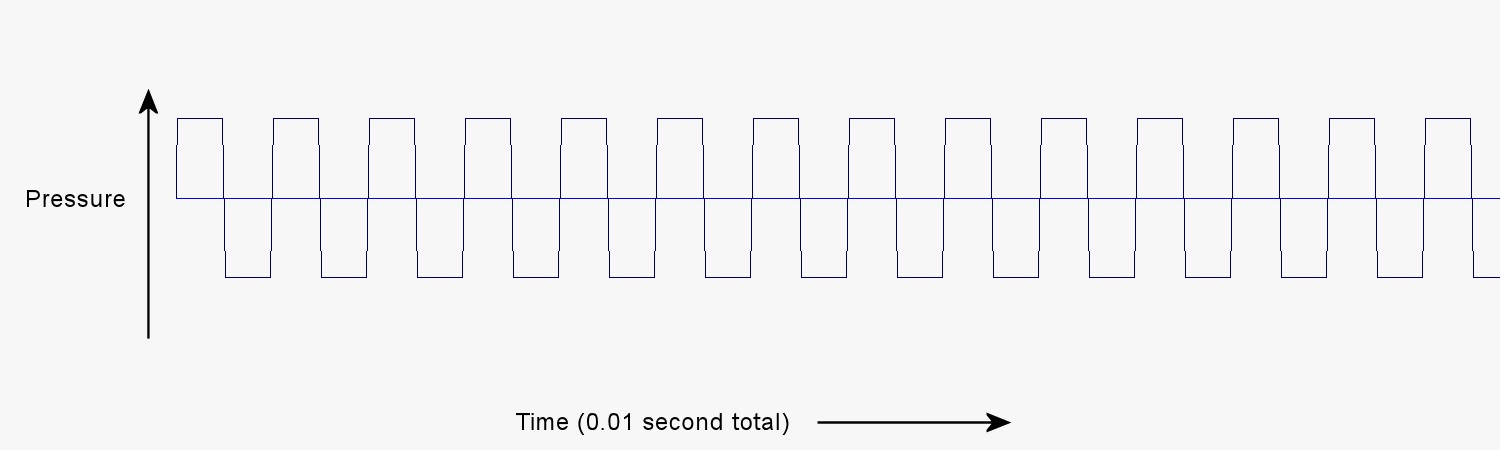
These four streams of pulses all have the same frequency, and the pitch we hear is the same for all of them. Yet, they do sound different. The difference in the sound is like the difference between the sound of a violin and the sound of a clarinet both playing the same pitch. That difference is called timbre. What makes the violin sound different from a clarinet playing the same pitch is that the shapes of the pressure pulses from each instrument is different from the shapes of the pulses from the other. To understand how and why different instruments produce pressure pulses of different shapes, it will be helpful to examine more closely the nature of the pulses themselves. In the process of doing this, we will discover some other characteristics of sound that we have not yet described.