Melody

Although rhythm can rouse the body to movement or lead it to repose, the deep influence that music can have on emotions comes from another aspect of music, namely melody. Melody is the soul of music. Melody can inspire sentiments of patriotism, hope, longing, and love. Melody is used in the religious expressions of most of the world’s faiths.

A melody is fundamentally a sequence of sounds having distinct and varied pitches and durations. Each of these sounds is called a note. It is more than just that, however. To form a melody, the sequence of pitches must be more than merely random. When a person hears a melody, the listener perceives the sequence of notes as a single entity. A melody forms a single idea, a musical idea. This is similar to the way that a sequence of words in a sentence forms an idea, although a musical idea is generally not as definite as a verbal idea. Furthermore, just as the meaning of a sequence of words is determined by the grammar of its language, there is a musical grammar that governs the meaning of a melody. Different languages have different grammars, and different cultures employ different musical grammars in constructing melodies. Perhaps the most complex of the cultural musical grammars is that of Western music, and some of that grammar will be explored later.

Just as a verbal expression can be composed of parts, phrases and clauses, so can a melody. The fundamental components of a melody are notes, sounds having definite pitches and durations. The relationship between the pitch of a note and the frequency of its vibration seems simple: the higher the frequency, the higher the pitch. Because the difference between two frequencies can be made infinitesimally small, there are an infinite number of pitches within the frequency range audible to humans. Yet, there is a point at which we cannot distinguish between the pitches of two notes of similar frequencies.

In order to have notes of perceptibly different pitches, there must be gaps between the frequencies of the notes. Nevertheless, there are a sizeable number of distinct audible pitches, far more than are used in music to construct a melody. Why do we use only a subset of them, and how is that subset selected?

Although a melody is a sequence of distinct pitches, it is not the pitches themselves that compose a particular melody. Instead, it is the intervals between the successive pitches that form the melody. The song is the same whether sung by a high soprano voice or a low bass voice.

What we recognize in the melody is the sequence of rising or falling intervals of particular sizes. In constructing a melody, it is the intervals between the notes that matter. So the question of which pitches from the infinite number available are selected for musical notes is actually a question of which intervals between pitches are selected, and of how they are chosen.

There is a primary interval which is universally recognized in all the world’s music. This interval can be heard when a string of a particular length is plucked followed by the plucking of the same string shortened to half its length.

A similar interval can be heard when the air in a pan pipe is set to vibrating, followed by the vibration of the air in a pipe half its length.

In both cases, the second, higher pitch seems distinctly different, yet somehow similar to the first. There is a physical reason for this apparent similarity; namely, the frequency of the second pitch is twice the frequency of the first.

There is another reason for the similarity. Neither the plucked string nor the vibrating air in the flute oscillate at a single frequency. The plucked string vibrates at multiple frequencies simultaneously. So too, the air in the flute vibrates at a collection of frequencies. This collection includes not only the lowest frequency, but also vibrations at higher frequencies. Prominent among these higher frequencies is the double. When you hear a plucked string, you hear vibrations at the string’s lowest frequency and vibrations at twice that frequency (as well as others). When you hear the half-string plucked, its lowest frequency is double the lowest frequency of the full string. But the full string produces the double frequency, too. This is why the tone from the half-string sounds somehow similar to the tone from the full string: both contain significant amounts of the same frequency. If you hear a tone that contains only a single frequency followed by a tone that contains only the double frequency, the similarity between the two tones is not as apparent as it is when the tones are generated from vibrations in physical objects such as strings or air.

The interval between two pitches could be expressed in various ways. One way would be to subtract the frequency of the lower pitch from that of the higher pitch. In the song, Mack the Knife, the two syllables of “jack-knife” are sung on two different pitches. When Ella Fitzgerald sang the song, the frequency she used for “jack” was about 430 Hz, and that for “knife” was about 390 Hz. The difference in frequencies was about 40 Hz. When Louis Armstrong sang the same words, he used about 290 Hz for “jack” and 260 Hz for “knife.” The difference for him was about 30 Hz. The frequency differences used by the two singers for the same interval in the song are different. Using frequency differences does not seem to be a good way to express the interval between pitches. We want the same interval, no matter if it is at high pitch or low pitch, to be expressed in the same way.

What turns out to be the most useful way to express intervals between pitches is to take the ratio of the two frequencies. The “jack-knife” interval in Mack the Knife, when sung by Ella Fitzgerald is 430 Hz / 390 Hz, which is 1.1. The same interval when sung by Louis Armstrong is 290 Hz / 260 Hz, which is also 1.1. When expressed as a ratio, the same interval in the song is expressed in the same way, whether the song is sung by Ella or Louis.

In music, the primary interval is the one between the pitch of a plucked full string and the pitch of half of the string when plucked. It is also the pitch of a panpipe flute and the pitch of a pipe half as long. In both cases, the fundamental frequency from the shorter string or pipe is twice the fundamental frequency from the longer string or pipe. The interval between the two pitches is described by the ratio of their fundamental frequencies, namely 2 to 1, or 2:1. The musical interval defined by a 2:1 frequency ratio is called an octave. The word “octave” sounds as though the number eight is somehow involved (consider octagon, an eight-sided shape, and octopus, an eight-armed sea creature), and it is. However, the origin of this name “octave” lies deep in the history of European music, and to describe its significance here would be to get ahead of the story.

Pitches composed of fundamental frequencies with ratios other than the octave ratio, 2:1, can also blend well together. Pitches having fundamental frequencies in a ratio of 3:2 also sound pleasantly together. Such pitches are produced when a string is plucked, then shortened to 2/3 its length and plucked again.

Similarly, the note from a pipe and the note from a pipe 2/3 as long have frequencies with a ratio of 3:2.

The interval between the pitches whose fundamental frequencies have a ratio of 3:2 is called a fifth. (Again, the name of this interval comes from the development of European music.)

When two pitches sound well together, such as those an octave apart or a fifth apart, they are said to be harmonious. (This is, incidentally, one of the few words used to describe sound that started as a description of sound, and then was applied by analogy to other situations, such as harmonious flavors and harmonious personalities. Most words used to describe music work in the other way; they apply primarily to non-musical situations and are used as analogies in music, such as high or low pitches and colorful sounds.) From the frequency ratio of the octave interval and the fifth interval, 2:1 and 3:2, respectively, one might get the idea that harmonious intervals have frequencies that are in the ratio of small whole numbers. This idea is correct to some degree. Another harmonious interval is that between the pitches with frequencies in the ratio of 5:4. A string shortened to 4/5 its full length will vibrate at a frequency 5/4 that of the full string.

A pipe that is 4/5 the full length will sound at a pitch with a frequency 5/4 that from the full-length pipe.

This interval is called a major third.

Yet another harmonious interval involves pitches with frequencies in a ratio of 5:3.

This interval is called the major sixth.

Yet another harmonious interval involves frequencies with a ratio of 9:8.

This interval is the major second.

The collection of five intervals, major 2nd, major 3rd, fifth, major 6th, and octave, define a set of six pitches. Together, this set of pitches form a collection of musical notes of rising pitch called a scale. This scale is called a pentatonic scale, because it contains five different pitches before reaching the double frequency, the octave.

A pentatonic scale forms the basis for melodies in nearly all cultures. Much of the music of Asia uses melodies constructed using a pentatonic scale, such as the Japanese folk song, Sakura Sakura.

Folk songs from many other cultures, from India, from Africa, and from Europe also involve a pentatonic scale. The Scottish folk song, “Auld Lang Syne,” and the American spiritual, “Swing Low Sweet Chariot,” both are based on a pentatonic scale.

Contemporary music, too, sometimes employs a pentatonic scale, such as “Whole Lotta Love” by Led Zeppelin.

Although the frequencies of the pitches in a pentatonic scale are in ratios of small whole numbers, this is not how the pitches were not originally selected. The pitches were selected for their sound, and the ways the sounds fit together. The frequency ratios were discovered long afterward. In fact, there is no single pentatonic scale. Different cultures have selected different sets whose pitches differ slightly, whose frequency ratios differ slightly from whole-number ratios. The origins of the various pentatonic scales are lost in the mists of time. One factor that may have influenced the pitch selections is the type of musical instruments used to create the sounds. Plucked strings have a different set of overtones from blown pipes. Both differ from the overtones from struck pieces of wood. The overtones of the notes influence how they sound together, when produced sequentially or simultaneously. A pentatonic scale produced “by ear” using plucked strings may well be different form a scale produced using blown pipes.

So if the pentatonic scale contains five intervals between a frequency and its double, why is the interval between a frequency and its double called an octave? Wouldn’t “pentave” be a better name? It might be, if the pentatonic scale were the only scale in use. However, various cultures have developed different scales that divide the gap between a frequency and its double into more than five intervals. Some Indian cultures use a scale that contains seven intervals (the Swara scale). Some Arabic music also employs a seven-note scale (maqam). More complex music in both of these cultures divide the scale into many more steps, sometimes as many as 24. The term octave derives from European music, in which the scale contains eight notes.

The European musical scale is based on a set of eight discrete pitches extending from a lowest pitch, the fundamental, to a pitch whose frequency is twice that of the fundamental. Over the course of the history of European music, the pitches have been selected in a variety of ways. One way they were selected is “by ear,” in which each pitch is chosen so that it fits pleasantly with its predecessor. When two pitches sound pleasant when one follows another, or when they sound simultaneously, the two pitches are said to be consonant. If two pitches produce an unpleasant sensation when one follows the other or when sounded together, the two pitches are called dissonant. Conversely, the pitches may be selected to reduce the number of unpleasant combinations (dissonances) when any two are sounded. Of course, how pleasant or unpleasant a combination of pitches may be depends on the listener. So whether two pitches are consonant or dissonant is a matter of opinion. Differing interpretations of “consonant” and “dissonant” have produced a variety of scales over the course of history.

There is general agreement, however, that pitches whose frequencies are in a ratio corresponding to small whole numbers have a pleasing, consonant sound. As the numbers in the ratios become larger, the consonance decreases. The ratio with the smallest whole numbers is 2:1, which corresponds to the octave, the most consonant interval. The ratio with the next smallest whole numbers is 3:2.

Selecting pitches based on consonance or dissonance concentrates on the pitches themselves and not on the intervals between them. Another method for choosing a collection of pitches is to concentrate on the intervals between the pitches. It begins with the fundamental interval, the octave, which is the interval between two pitches whose frequencies differ by a factor of two. These frequencies can be represented as f and 2f. This octave interval is divided into two equal intervals. The frequency that lies in the middle between f and 2f is the average of the two, (f + 2f)/2, which is 3/2 f. Then the lower of the two new intervals is divided itself into two equal intervals. The frequency of the pitch at the middle of the lower interval is (f + 3/2 f)/2, which is 5/4 f. So far, there are four pitches, and the following video shows how all of the intervals between them are in small, whole-number ratios – they are consonant.

The highest pitch has a frequency of 2f. The central pitch has a frequency of 3/2 f. The ratio between these frequencies is 2f / (3/2 f), which is 4/3. A frequency of with the same relationship to the lowest frequency, namely 4/3 f, is added to the collection, which forms additional consonant intervals.

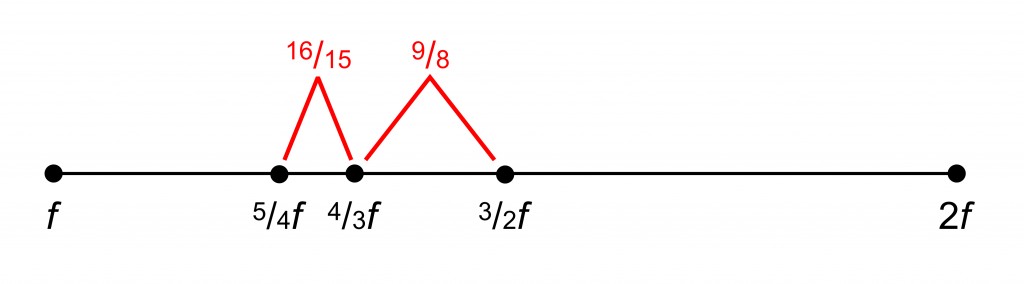
More consonant intervals are created by adding the frequency at 5/3 f.

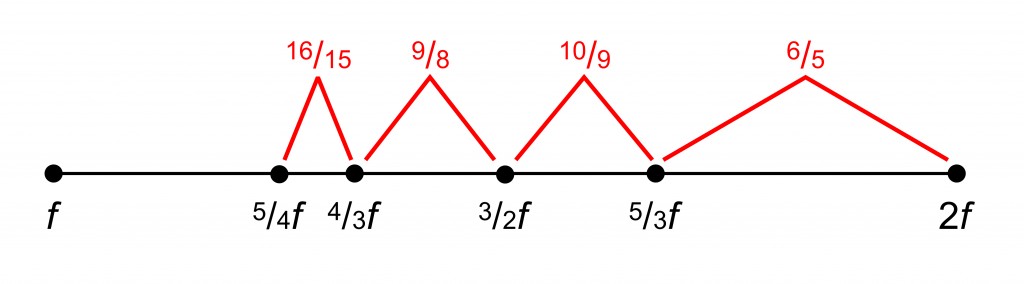
The interval between f and 5/4 f is large and can be divided into two equal intervals by adding a frequency at the average, ( 2f + 5/4 f ) / 2, which is 9/8 f. This adds further consonant intervals.

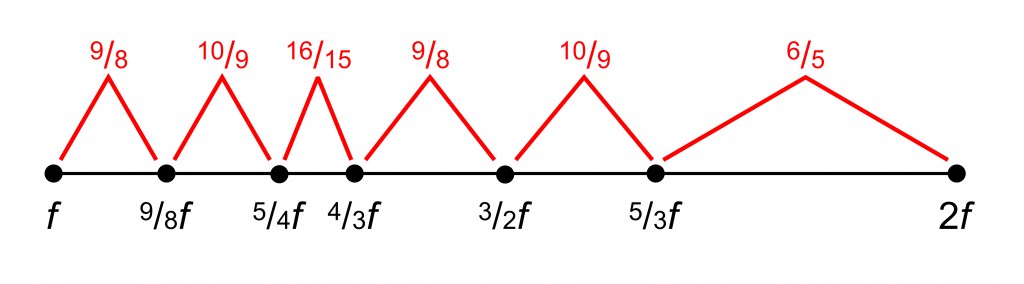
The interval between 5/3 f and 2 f is also larger than any of the others, and this too can be divided to produce more consonant intervals by adding the frequency 15/8 f.

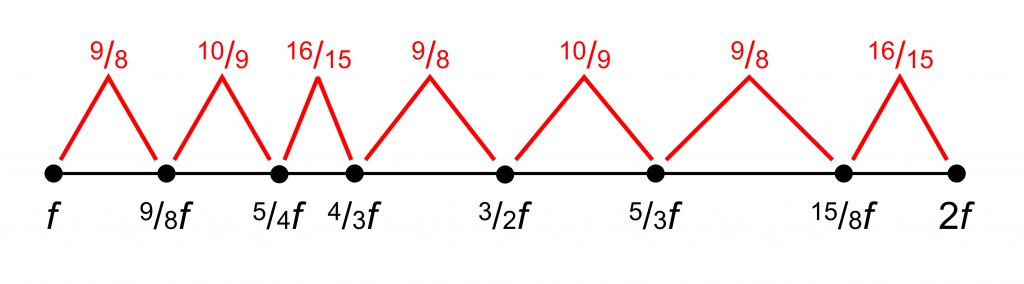
This collection of pitches is called the just diatonic scale, and forms the basis of the major scale used in much of Western music. Because this collection contains 8 pitches with frequencies from f to 2f, the interval from f to 2f is called an octave. Similarly, the frequency span from f to 3/2 f contains five pitches, so this span is called a fifth.

In this set of eight pitches, there are sequential intervals of effectively two different sizes. There are two smaller intervals between the 3rd and 4th pitches and between the 7th and 8th pitches. The ratios of the frequencies in these two intervals are both 16/15, or 1.125. There are five larger intervals, between the 1st and 2nd, 2nd and 3rd, 4th and 5th, 5th and 6th, and 6th and 7th frequencies. The ratios of the frequencies in these intervals are either 9/8 (1.125) or the similar 10/9 (1.111). The larger intervals are about twice the size of the smaller intervals. Each of these larger intervals can be divided into two by adding an intermediate frequency. To keep the number of consonances at a maximum, frequencies that form relatively small whole number ratios are added, namely the following five frequencies: ⁶/₅f, ⁹/₅f, ²⁵/₁₆f, ²⁵/₂₄f, and ⁴⁵/₃₂f.

This selection results in twelve intervals that are similar but not identical. This collection of pitches is called the just chromatic scale. It is called chromatic because the pitches that are added to the 8-note scale to form the 12-note scale were thought of as shadings or tints (chromas) of the original 8 notes. It is a just scale, because the pitches are selected so that their frequencies produce the greatest number of small whole-number ratios.

Because the intervals between frequencies in the just chromatic scale are not all the same, the actual frequencies in the scale depend on the fundamental frequency, f. For example, if the fundamental frequency is 260 Hz (near middle C), then the frequencies of the pitches on the just scale are those shown in the first row in the chart below. However, if the fundamental frequency is chosen to be that of the third pitch from the first row, some of the subsequent pitches match those of the first series, but others do not (the highlighted ones).

Changing the fundamental pitch during a piece of music is a technique that was adopted in Western music to add variety to musical compositions. The fact that the pitches did not match from one set to the next did not pose a problem for voices or for instruments that can play any pitch in their ranges, such as string instruments in the viol family. However, instruments whose pitches were fixed, most notably keyboard instruments, had a problem when the fundamental frequency changed. They could play only one set of frequencies. So, if the fundamental frequency changed during a piece of music, either they would have to avoid the pitches that they could not play, or when they played their pitches they would be out of tune with other instruments. A solution to this problem was devised by adjusting the intervals in the chromatic scale to be all of the same size. Since there are 12 intervals, the size of each interval is one-twelfth of the entire span. This means that each frequency is the twelfth root of 2 (1.0595) times the previous frequency. This results in what is called a well-tempered scale.

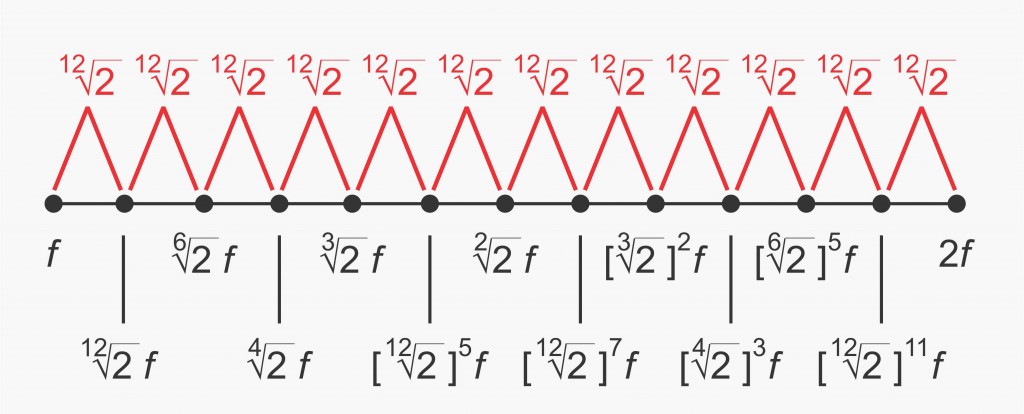
With this scale, changing the fundamental frequency from one pitch to another produces a collection of pitches with the same frequencies as the original. This allows changes in the fundamental to be played on keyboard instruments. However, none of the frequencies is in a ratio of small whole numbers to any other frequency, which means that none of the combinations of pitches (except the octave) is completely consonant. This is the price that has been paid for the convenience of keyboard players. There was considerable controversy in the 15th through 17th Centuries over whether sacrificing consonance for convenience was worth it. Consensus has developed around the well-tempered scale, perhaps because of one of its most influential advocates, Johann Sebastian Bach, who composed two monumental sets of keyboard pieces in the two books of The Well-Tempered Klavier. Each book contains a set of 24 pieces, and each piece is composed in a different one of the twelve keys, both major and minor versions, derived from the well-tempered chromatic scale.

The chromatic scale divides the octave into twelve equal intervals.

Each of these intervals is called a semitone. Two semitones make a whole tone. The chromatic scale provides a set of 12 notes from which 8 can be chosen to form an octave scale. Different subsets of 8 notes produce different scales. The different scales are called modes. Different modes have different affective properties; that is, some modes sound happy, others sound sad, yet others sound solemn. The most common mode is the Ionian mode, also called the major scale. It is constructed using intervals in sequence from the lowest note: whole tone, whole tone, half tone, whole tone, whole tone, whole tone, and half tone. The intervals can be represented as 2 : 2 : 1 : 2 : 2 : 2 : 1, where 1 represents a semitone and 2 a whole tone.

This is the most frequently used scale in European music since the Renaissance, and it is particularly common in popular music. More consonant combinations can be formed from the notes in this scale than in any other 8-note scale. The pleasing consonances give music using this scale a pleasant, even happy, feel.

Another common selection of notes from the chromatic scale forms the Aeolian mode, also called the minor scale. In this scale the intervals are 2 : 1 : 2 : 2 : 1 : 2 : 2.

Music that uses the minor scale sounds solemn or even sad. Examples of music using the minor scale are the medieval hymn “O Come, O Come, Emmanuel” and “Electrical Storm” by U2.

There are many ways to select a subset of 8 notes from the 12 of the chromatic scale. There are many different possible scales in addition to the major and minor scales, although none is as commonly used as these. The elaboration of different scales in European music allowed, and was perhaps driven by, modifications in a melody that left the melody recognizable, yet changed. These modifications prevent a repeated melody from becoming dull. They permit a melody to be explored and developed, so its emotional content can be advanced and expanded.

No matter how engaging a melody is, there comes a time when its interest wanes. No musical expressions of any significant length can get away with using only one melody. Popular songs generally have a chorus as well as verses, and these have different melodies. This excerpt from the Beatles’ song “Penny Lane” begins with the verse melody, continues to the chorus melody, and then returns to the verse melody.

The alternations between the verse melody and the chorus melody avoid the monotony of repeating the same melody over and over.

Multiple melodies do not need to occur at different times, as they do in a song with verse and chorus. Humans have a remarkable ability to distinguish two separate melodies simultaneously, when the notes of one melody are very different in pitch from the notes of the other melody. This ability of humans to segregate a series of notes that have large intervals between them into two separate melodies was exploited particularly in 17th- and 18th-century European music. The fugue is a type of music that developed at that time in which melodies are played simultaneously. One of the most famous of such fugues is the D-minor fugue by J. S. Bach. The following video contains a section of this fugue in which each melody is represented visually in a different color and the pitches are arranged vertically with high pitches above and lower pitches below.

Our tendency to separate notes with large intervals between them into separate melodies suggests that, for a sequence of notes to be perceived as a melody, the intervals should be small. This seems to be the case. Nearly all memorable melodies consist of progressions of notes with small intervals between each note and its successor. An occasional large interval can add some interest or drama to a melody, but if all intervals are large, we don’t perceive a melody at all. What we perceive in that case is a sequence seemingly random notes – the notes don’t come together into a unit. Yet, not every series of notes with small intervals makes a memorable melody. What makes a memorable melody is a question whose answer is elusive.